Inversion

Fomel (2002) shows that a possible solution to the slope estimation problem is obtained by minimizing the non-linear function

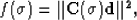$$f(\sigma)=\Vert\bf{C(\sigma)d}\Vert^2,$$ (13)

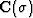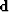where $\bf{C(\sigma)}$ is the operator convolving the data with the 2-D filter C_n(Z_t,Z_h) and ${\bf d}$ is the known data. Fomel (2002) proposes iterating with a Gauss-Newton algorithm:

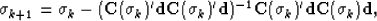$$\sigma_{k+1} = \sigma_{k} - ({\bf C}(\sigma_k)'{\bf d C}(\s... ...{\bf d})^{-1}{\bf C}(\sigma_k)'{\bf d}{\bf C}(\sigma_k){\bf d},$$ (14)

where the step is estimated with a conjugate gradient method. One problem with this approach is that it converges well only if we are close enough to the true solution. Another problem stems from the fact that no line search in the gradient direction is implemented. Therefore, this method might oscillate close to the solution.

To make the dip estimation more robust and also to incorporate the possibility to bound-constrain the dips, the L-BFGS-B method is used instead of the Gauss-Newton approach. For the L-BFGS-B method, similar to BFGS, we need to estimate the function and its gradient. Incorporating a regularization operator 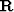${\bf R}$ that penalizes differences between adjacent dip values, the objective function becomes

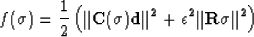$$f(\sigma)=\frac{1}{2}\left ( \Vert\bf{C(\sigma)d}\Vert^2+\epsilon^2\Vert{\bf R}\sigma\Vert^2 \right )$$ (15)

and the gradient is

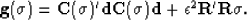$${\bf g}(\sigma)={\bf C}(\sigma)'{\bf d}{\bf C}(\sigma){\bf d}+\epsilon^2 {\bf R'R\sigma}.$$ (16)

The dips can be then estimated reliably. In the next section, the L-BFGS-B method is illustrated on different examples. These examples illustrate that the bound constrained optimization improves the dip values when events with different local slopes overlap.