




Next: Derivation of Snell Resampling
Up: Least-squares joint imaging of
Previous: Conclusions on the 3-D
HEMNO Equivalence with Levin and Shah's Equations
In this appendix, I prove that the HEMNO equation is equivalent to Levin and
Shah's traveltime equation Levin and Shah (1977) in the limit of small dip
angle. They show that in a constant velocity medium with dipping target
reflector and multiple generator, the moveout equation of the ``S102G'' pegleg
multiple (see Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is:
) is:
| ![\begin{displaymath}
t^2 = \left[\tau^* \cos{\theta} + \tau \cos{\phi}\right]^2
...
...+\theta)}}{V} - \tau^* \sin{\theta} - \tau \sin{\phi}\right]^2,\end{displaymath}](img148.gif) |
(39) |
where 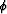 and
and 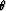 are the dip angle (in radians) of the multiple
generator and target reflector, respectively.
are the dip angle (in radians) of the multiple
generator and target reflector, respectively. 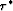 and
and  are the
zero-offset traveltimes to the two reflectors, x is offset, and V is the
medium velocity. For small dip angles (i.e., less than 5 degrees), we can make
the small angle approximation for angles
are the
zero-offset traveltimes to the two reflectors, x is offset, and V is the
medium velocity. For small dip angles (i.e., less than 5 degrees), we can make
the small angle approximation for angles 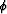 ,
, 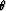 , and
, and 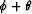 to
update equation (
to
update equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) accordingly:
) accordingly:
| ![\begin{displaymath}
t^2 = \left[\tau^* + \tau \right]^2
+ \left[\frac{x}{V} - \tau^* \theta - \tau \phi\right]^2.\end{displaymath}](img151.gif) |
(40) |
Multiplying out the squares in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and collecting
terms gives:
) and collecting
terms gives:
| ![\begin{displaymath}
t^2 = \left[\tau^* + \tau \right]^2 + \frac{x^2}{V^2}
- 2\...
... - 2\frac{\phi \tau x}{V}
+ (\tau^* \theta)^2 + (\tau \phi)^2.\end{displaymath}](img152.gif) |
(41) |
The 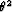 and
and 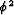 terms are negligible for small angles, so we can
ignore these terms and further simplify equation (
terms are negligible for small angles, so we can
ignore these terms and further simplify equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
| ![\begin{displaymath}
t^2 = \left[\tau^* + \tau \right]^2 + \frac{x^2}{V^2}
- 2\frac{ (\theta \tau^* + \phi \tau) x }{V}.\end{displaymath}](img155.gif) |
(42) |
I will now show that the HEMNO equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is equivalent to the
Levin/Shah equation (
) is equivalent to the
Levin/Shah equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) under the constant velocity and small
dip angle assumptions. First I make some preliminary definitions. In a
constant-velocity medium, the expression for xp, equation (
) under the constant velocity and small
dip angle assumptions. First I make some preliminary definitions. In a
constant-velocity medium, the expression for xp, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
simplifies to:
),
simplifies to:
| 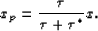 |
(43) |
Then x-xp, which will be needed later, simplifies to:
| 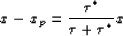 |
(44) |
Since the reflectors in this derivation are assumed planar and the velocity is
assumed constant, using equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can
directly write the (two-way) zero offset traveltime to the seabed and subsea
reflection at any midpoint as a function of the corresponding zero-offset
traveltimes at the midpoint location, y0:
), we can
directly write the (two-way) zero offset traveltime to the seabed and subsea
reflection at any midpoint as a function of the corresponding zero-offset
traveltimes at the midpoint location, y0:
| 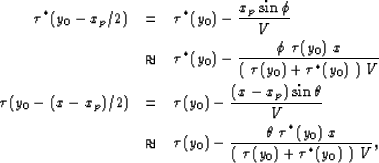 |
|
| (45) |
| |
| (46) |
where the small angle approximation was employed as before. Substituting the
zero-offset traveltimes (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into the
HEMNO equation (
) into the
HEMNO equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields:
) yields:
| 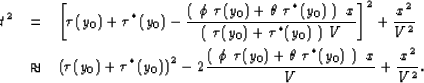 |
(47) |
| (48) |
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is equivalent to equation
(
) is equivalent to equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Therefore, we have proven the equivalence of the
moveout equations of the true and approximate raypaths shown in Figure
). Therefore, we have proven the equivalence of the
moveout equations of the true and approximate raypaths shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , subject to the small dip angle approximation. As
before,
, subject to the small dip angle approximation. As
before, 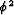 and
and 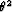 terms were dropped in going from equation
(
terms were dropped in going from equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to equation (
) to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Although explicit
seabed and subsea reflector dip angles,
). Although explicit
seabed and subsea reflector dip angles, 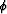 and
and 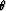 , are contained in
equation (
, are contained in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), they were introduced only to show equivalence
to equation (
), they were introduced only to show equivalence
to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Locally-planar reflectors are not
required to implement equation (
). Locally-planar reflectors are not
required to implement equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).





Next: Derivation of Snell Resampling
Up: Least-squares joint imaging of
Previous: Conclusions on the 3-D
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is:
) is:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is:
) is:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) accordingly:
) accordingly:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and collecting
terms gives:
) and collecting
terms gives:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is equivalent to the
Levin/Shah equation (
) is equivalent to the
Levin/Shah equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) under the constant velocity and small
dip angle assumptions. First I make some preliminary definitions. In a
constant-velocity medium, the expression for xp, equation (
) under the constant velocity and small
dip angle assumptions. First I make some preliminary definitions. In a
constant-velocity medium, the expression for xp, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
simplifies to:
),
simplifies to:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can
directly write the (two-way) zero offset traveltime to the seabed and subsea
reflection at any midpoint as a function of the corresponding zero-offset
traveltimes at the midpoint location, y0:
), we can
directly write the (two-way) zero offset traveltime to the seabed and subsea
reflection at any midpoint as a function of the corresponding zero-offset
traveltimes at the midpoint location, y0:
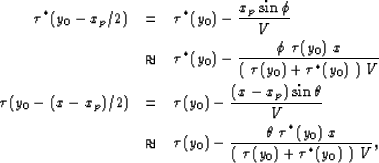
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into the
HEMNO equation (
) into the
HEMNO equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields:
) yields:
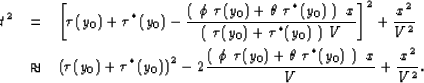
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is equivalent to equation
(
) is equivalent to equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Therefore, we have proven the equivalence of the
moveout equations of the true and approximate raypaths shown in Figure
). Therefore, we have proven the equivalence of the
moveout equations of the true and approximate raypaths shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , subject to the small dip angle approximation. As
before,
, subject to the small dip angle approximation. As
before, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to equation (
) to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Although explicit
seabed and subsea reflector dip angles,
). Although explicit
seabed and subsea reflector dip angles, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), they were introduced only to show equivalence
to equation (
), they were introduced only to show equivalence
to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Locally-planar reflectors are not
required to implement equation (
). Locally-planar reflectors are not
required to implement equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).