




Next: Differential Geometric Spreading
Up: Particular Implementation of LSJIMP
Previous: Amplitude corrections for pegleg
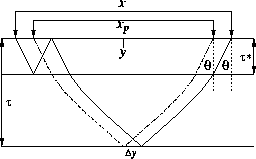
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the fact that in a v(z) medium, there
exists a single offset xp such that a pegleg with offset x and primary with
offset xp are physically invariant with respect to AVO behavior and, assuming
perfect elasticity in the top layer (often water), to anelastic attenuation.
Since the pegleg multiple and primary in Figure
illustrates the fact that in a v(z) medium, there
exists a single offset xp such that a pegleg with offset x and primary with
offset xp are physically invariant with respect to AVO behavior and, assuming
perfect elasticity in the top layer (often water), to anelastic attenuation.
Since the pegleg multiple and primary in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) have the
same emergence angle,
have the
same emergence angle, 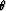 , the time dip, or ``stepout'' of the two events
is the same at x and xp. In Appendix
, the time dip, or ``stepout'' of the two events
is the same at x and xp. In Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I derive
the following expression for xp, where
, I derive
the following expression for xp, where 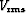 ,
, 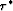 , and
, and
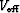 were defined in Section
were defined in Section ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) :
:

| 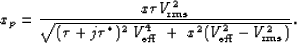 |
(21) |
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) defines, for a
) defines, for a 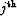 -order pegleg, a
time-variable compression of the offset axis, which I denote ``Snell
Resampling''. The name is derived from Ottolini's 1982
``Snell Traces'' - a resampling of multi-offset reflection data along curves of
constant stepout. Note that in a constant velocity medium,
-order pegleg, a
time-variable compression of the offset axis, which I denote ``Snell
Resampling''. The name is derived from Ottolini's 1982
``Snell Traces'' - a resampling of multi-offset reflection data along curves of
constant stepout. Note that in a constant velocity medium,
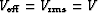 , and equation (
, and equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) reduces to the
radial trace resampling used by Taner (1980) for the long-period
deconvolution of peglegs.
) reduces to the
radial trace resampling used by Taner (1980) for the long-period
deconvolution of peglegs.
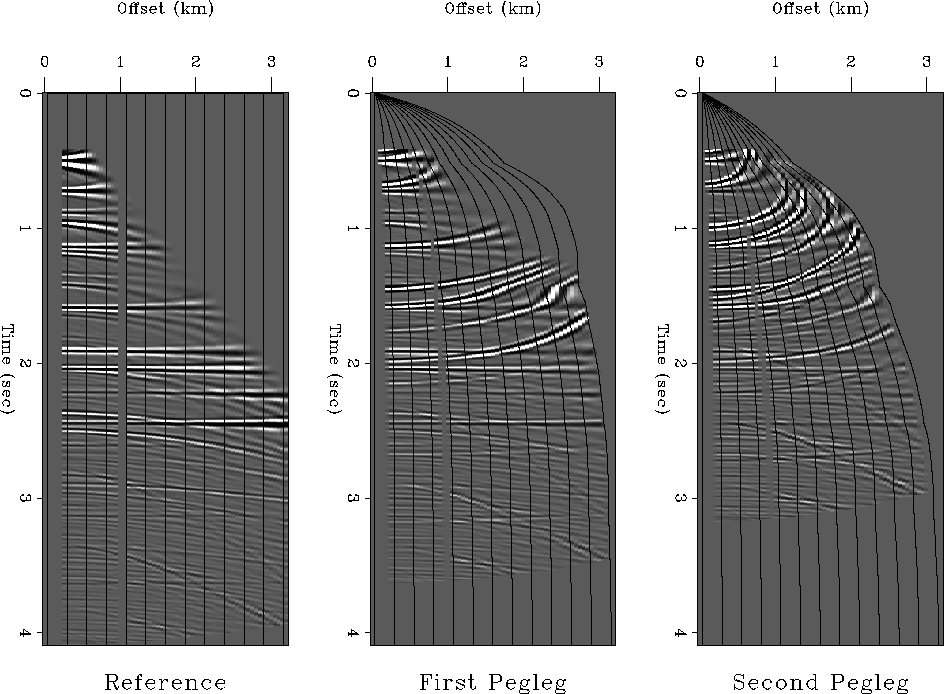
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates application of Snell Resampling to a
synthetic CMP gather. From the Figure, we see that Snell Resampling is an
important vehicle for the exploitation of the additional information contained in
the multiples. Notice how energy from the multiples is spread into the coverage
gaps at near offsets and at 1.0 km offset. Snell Resampling moves energy from
the multiples to the offset corresponding to its reflection angle at the target.
illustrates application of Snell Resampling to a
synthetic CMP gather. From the Figure, we see that Snell Resampling is an
important vehicle for the exploitation of the additional information contained in
the multiples. Notice how energy from the multiples is spread into the coverage
gaps at near offsets and at 1.0 km offset. Snell Resampling moves energy from
the multiples to the offset corresponding to its reflection angle at the target.
snell.hask
Figure 5 Snell Resampling demonstration. Left to
right: a synthetic CMP gather after NMO for primaries and for first- and
second-order peglegs, respectively. Snell Resampling (plus normalization to
account for offset axis compression) was applied to the right two panels. The
black lines illustrate the transformation's horizontal compression. The raw
data has five unrecorded near offset traces and two dead traces at medium
offsets.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





Graphically (Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we may infer that the shift in
midpoint,
), we may infer that the shift in
midpoint, 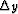 , of the reflection points of the primary and first-order
pegleg is:
, of the reflection points of the primary and first-order
pegleg is:
| 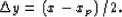 |
(22) |
As a function of time, 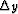 decreases asymptotically to zero at infinite
depth from a maximum of x/4 at the seabed. The deeper the reflector, the
smaller
decreases asymptotically to zero at infinite
depth from a maximum of x/4 at the seabed. The deeper the reflector, the
smaller 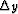 becomes. Similar expressions may be easily derived for
multiples of other types and orders.
becomes. Similar expressions may be easily derived for
multiples of other types and orders.
For peglegs arising from sub-seabed reflectors, the assumption of perfect
elasticity for the multiple bounce breaks down. To some extent, however, the
additional attenuation suffered by the multiple can, to first order, be treated
as a decrease in reflection coefficient.





Next: Differential Geometric Spreading
Up: Particular Implementation of LSJIMP
Previous: Amplitude corrections for pegleg
Stanford Exploration Project
5/30/2004
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates the fact that in a v(z) medium, there
exists a single offset xp such that a pegleg with offset x and primary with
offset xp are physically invariant with respect to AVO behavior and, assuming
perfect elasticity in the top layer (often water), to anelastic attenuation.
Since the pegleg multiple and primary in Figure
illustrates the fact that in a v(z) medium, there
exists a single offset xp such that a pegleg with offset x and primary with
offset xp are physically invariant with respect to AVO behavior and, assuming
perfect elasticity in the top layer (often water), to anelastic attenuation.
Since the pegleg multiple and primary in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) have the
same emergence angle,
have the
same emergence angle, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I derive
the following expression for xp, where
, I derive
the following expression for xp, where ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) :
:
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)