




Next: Wave-equation migration velocity analysis
Up: Theory
Previous: Theory
Consider a (nonlinear) function 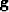 mapping
one element of the functional model space
mapping
one element of the functional model space 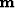 to
one element of the functional data space
to
one element of the functional data space 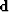 :
:
| 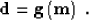 |
(1) |
The tangent linear application to 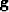 at point
at point 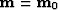 is
a linear operator
is
a linear operator 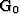 defined by the expansion
defined by the expansion
| 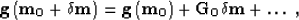 |
(2) |
where 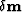 is a small perturbation in the model space.
The tangent linear application
is a small perturbation in the model space.
The tangent linear application 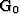 is also known under
the name of Fréchet derivative of
is also known under
the name of Fréchet derivative of 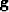 at point
at point 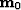 Tarantola (1987).
Tarantola (1987).
Equation (2) can be written formally as
| 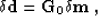 |
(3) |
where
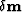 is a perturbation in the model space, and
is a perturbation in the model space, and
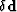 is a perturbation in the image space.
If we denote by
is a perturbation in the image space.
If we denote by 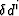 the ith component of
the ith component of 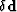 ,
and by
,
and by 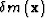 an infinitesimal element of
an infinitesimal element of 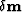 at location
at location  , we can write
, we can write
| 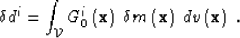 |
(4) |
G0i is, by definition, the integral kernel
of the Fréchet derivative 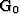 ,
,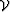 is the volume under investigation,
d v is a volume element of
is the volume under investigation,
d v is a volume element of 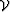 and
and  is the
integration variable over
is the
integration variable over 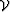 .The sensitivity kernel, a.k.a. Fréchet derivative kernel ,
G0i expresses the sensitivity of
.The sensitivity kernel, a.k.a. Fréchet derivative kernel ,
G0i expresses the sensitivity of
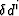 to a perturbation of
to a perturbation of 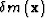 for
an arbitrary location
for
an arbitrary location  in the volume
in the volume 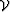 .
.
Sensitivity kernels occur in every inverse problem and have different meanings
depending of the physical quantities involved:
- For wideband traveltime tomography
Bishop et al. (1985); Kosloff et al. (1996); Stork (1992),
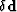 is represented by traveltime differences
between recorded and computed traveltimes in a reference medium.
The sensitivity kernels are infinitely-thin rays
computed by ray tracing in the background medium.
is represented by traveltime differences
between recorded and computed traveltimes in a reference medium.
The sensitivity kernels are infinitely-thin rays
computed by ray tracing in the background medium.
- For finite-frequency traveltime tomography
Dahlen et al. (2000); Hung et al. (2000); Marquering et al. (1999); Rickett (2000),
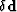 is represented by time shifts
measured by crosscorelation between the recorded wavefield
and a wavefield computed in a reference medium.
The sensitivity kernels are represented by hollow fat rays
(a.k.a. ``banana-doughnuts'') which depend on the background medium.
is represented by time shifts
measured by crosscorelation between the recorded wavefield
and a wavefield computed in a reference medium.
The sensitivity kernels are represented by hollow fat rays
(a.k.a. ``banana-doughnuts'') which depend on the background medium.
- For wave-equation tomography
Pratt (1999); Woodward (1992),
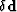 is represented by perturbations
between the recorded wavefield and the computed wavefield
in a reference medium.
The sensitivity kernels are represented by fat rays with similar forms
for either the Born or Rytov approximation.
is represented by perturbations
between the recorded wavefield and the computed wavefield
in a reference medium.
The sensitivity kernels are represented by fat rays with similar forms
for either the Born or Rytov approximation.
- For wave-equation migration velocity analysis
Biondi and Sava (1999); Sava and Biondi (2004a,b); Sava and Fomel (2002),
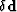 is represented by image perturbations.
The sensitivity kernels are discussed in the following sections.
is represented by image perturbations.
The sensitivity kernels are discussed in the following sections.





Next: Wave-equation migration velocity analysis
Up: Theory
Previous: Theory
Stanford Exploration Project
5/23/2004