




Next: Examples
Up: Theory
Previous: Fréchet derivative integral kernels
Wave-equation migration velocity analysis (WEMVA)
is based on a linear relation established between
perturbations of the slowness model 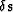 and
perturbations of migrated images
and
perturbations of migrated images 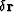 .
.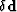 and
and 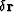 correspond, respectively, to
correspond, respectively, to 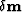 and
and 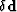 in equation (3).
in equation (3).
Formally, we can write
| 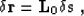 |
(5) |
where 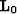 is the linear first-order Born
wave-equation MVA operator.
The operator
is the linear first-order Born
wave-equation MVA operator.
The operator 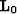 incorporates all first-order scattering
and extrapolation effects for media of arbitrary complexity.
The major difference between WEMVA and
wave-equation tomography is that
incorporates all first-order scattering
and extrapolation effects for media of arbitrary complexity.
The major difference between WEMVA and
wave-equation tomography is that 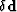 is formulated
in the image space for the former as opposed to the
data space for the later. Thus, with WEMVA we are able
to exploit the power of residual migration in perturbing
migrated images - a goal which is much harder to achieve
in the space of the recorded data.
is formulated
in the image space for the former as opposed to the
data space for the later. Thus, with WEMVA we are able
to exploit the power of residual migration in perturbing
migrated images - a goal which is much harder to achieve
in the space of the recorded data.
By construction, the linear operator 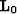 depends on
the wavefield computed by extrapolation of the surface
data using the background slowness,
which corresponds to
depends on
the wavefield computed by extrapolation of the surface
data using the background slowness,
which corresponds to 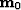 in equation (2).
Thus, the operator
in equation (2).
Thus, the operator 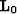 depends directly on the type of
recorded data and its frequency content,
and it also depends on the background slowness model.
Thus, the main elements that control the shape
of the sensitivity kernels are
depends directly on the type of
recorded data and its frequency content,
and it also depends on the background slowness model.
Thus, the main elements that control the shape
of the sensitivity kernels are
- the frequency content of the background wavefield,
- the type of source from which we generate the background
wavefield (e.g. point source, plane wave), and
- the type of perturbation introduced in the image space,
which for this problem corresponds to the data space.
In our examples, we define two types of image perturbations:
a purely kinematic type 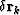 , implemented simply as a derivative
of the image with respect to depth, which can be implemented as
a multiplication in the depth wavenumber domain
Sava and Biondi (2004a,b) as follows:
, implemented simply as a derivative
of the image with respect to depth, which can be implemented as
a multiplication in the depth wavenumber domain
Sava and Biondi (2004a,b) as follows:
| 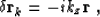 |
(6) |
and a purely dynamic type 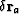 , implemented by
scaling the reference image
, implemented by
scaling the reference image  with
an arbitrary number:
with
an arbitrary number:
| 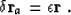 |
(7) |
In both cases, the perturbations are limited to
a small portion of the image.
The main difference between 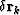 and
and 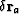 is given by the
is given by the 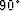 phase-shift between the
two image perturbations.
phase-shift between the
two image perturbations.





Next: Examples
Up: Theory
Previous: Fréchet derivative integral kernels
Stanford Exploration Project
5/23/2004
![]() depends on
the wavefield computed by extrapolation of the surface
data using the background slowness,
which corresponds to
depends on
the wavefield computed by extrapolation of the surface
data using the background slowness,
which corresponds to ![]() in equation (2).
Thus, the operator
in equation (2).
Thus, the operator ![]() depends directly on the type of
recorded data and its frequency content,
and it also depends on the background slowness model.
Thus, the main elements that control the shape
of the sensitivity kernels are
depends directly on the type of
recorded data and its frequency content,
and it also depends on the background slowness model.
Thus, the main elements that control the shape
of the sensitivity kernels are
![]() , implemented simply as a derivative
of the image with respect to depth, which can be implemented as
a multiplication in the depth wavenumber domain
Sava and Biondi (2004a,b) as follows:
, implemented simply as a derivative
of the image with respect to depth, which can be implemented as
a multiplication in the depth wavenumber domain
Sava and Biondi (2004a,b) as follows: