Next: Compliance formulation
Up: Berryman: Poroelastic fluid effects
Previous: RELATIONS FOR ANISOTROPY IN
The 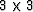 system (10)
can be analyzed fairly easily, and in
particular the eigenfunctions and eigenvalues of this system can be
obtained in general. However, such general results do not provide much
physical insight into the problem we are trying to study, so instead of
proceeding in this direction we will now restrict attention to
transversely isotropic materials. This case is relevant to many
layered earth materials and also industrial systems, and it
is convenient because we can immediately eliminate one of the
eigenvectors from further consideration. Three mutually orthogonal
(but unnormalized) vectors of interest are:
system (10)
can be analyzed fairly easily, and in
particular the eigenfunctions and eigenvalues of this system can be
obtained in general. However, such general results do not provide much
physical insight into the problem we are trying to study, so instead of
proceeding in this direction we will now restrict attention to
transversely isotropic materials. This case is relevant to many
layered earth materials and also industrial systems, and it
is convenient because we can immediately eliminate one of the
eigenvectors from further consideration. Three mutually orthogonal
(but unnormalized) vectors of interest are:
| 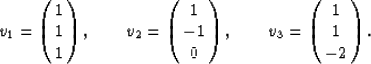 |
(12) |
Treating these vectors as stresses, the first corresponds to a
simple hydrostatic stress, the second to a planar shear stress, and
the third to a pure shear stress applied uniaxially along the z-axis
(which would also be the symmetry axis for a layered system, but we
are not treating such layered systems here).
Transverse isotropy of the system under consideration
requires: s11 = s22,
s13 = s23, and for the poroelastic problem 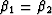 . Thus, it is immediately apparent that the planar shear
stress v2 is an eigenvector of the system, and furthermore it
results in no contribution from the pore fluid. Therefore,
this vector will be of no further interest here, and the system can
thereby be reduced to
. Thus, it is immediately apparent that the planar shear
stress v2 is an eigenvector of the system, and furthermore it
results in no contribution from the pore fluid. Therefore,
this vector will be of no further interest here, and the system can
thereby be reduced to 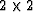 .
.
![]() system (10)
can be analyzed fairly easily, and in
particular the eigenfunctions and eigenvalues of this system can be
obtained in general. However, such general results do not provide much
physical insight into the problem we are trying to study, so instead of
proceeding in this direction we will now restrict attention to
transversely isotropic materials. This case is relevant to many
layered earth materials and also industrial systems, and it
is convenient because we can immediately eliminate one of the
eigenvectors from further consideration. Three mutually orthogonal
(but unnormalized) vectors of interest are:
system (10)
can be analyzed fairly easily, and in
particular the eigenfunctions and eigenvalues of this system can be
obtained in general. However, such general results do not provide much
physical insight into the problem we are trying to study, so instead of
proceeding in this direction we will now restrict attention to
transversely isotropic materials. This case is relevant to many
layered earth materials and also industrial systems, and it
is convenient because we can immediately eliminate one of the
eigenvectors from further consideration. Three mutually orthogonal
(but unnormalized) vectors of interest are: