Next: Eigenvectors for Transverse Isotropy
Up: Berryman: Poroelastic fluid effects
Previous: FLUID-SATURATED POROELASTIC ROCKS
Gassmann (1951), Brown and Korringa (1975), and others have considered the
problem of obtaining effective constants for anisotropic poroelastic
materials when the pore fluid is confined within the pores. The
confinement condition amounts to a constraint that the increment of
fluid content 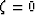 , while the external loading
, while the external loading  is changed
and the pore-fluid pressure pf is allowed to respond as necessary and
thus equilibrate.
is changed
and the pore-fluid pressure pf is allowed to respond as necessary and
thus equilibrate.
To provide an elementary derivation of the Gassmann equation for
anisotropic materials, we consider the anisotropic generalization
of (1)
| 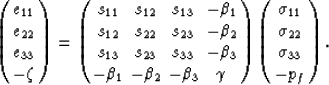 |
(9) |
Three shear contributions have been immediately excluded from consideration
since they can easily be shown not to interact
mechanically with the fluid effects. This form is not
completely general in that it includes orthorhombic, cubic, hexagonal,
and all isotropic systems, but excludes triclinic, monoclinic,
trigonal, and some tetragonal systems that would have some nonzero
off-diagonal terms in the full elastic matrix. Also, we have
assumed that the
material axes are aligned with the spatial axes. But this latter
assumption is not significant for the derivation that follows.
Such an assumption is important when properties of laminated materials
having arbitrary orientation relative to the spatial axes need to be
considered, but we do not treat this more general problem here.
If the fluid is confined (or undrained on the time scales of
interest), then 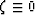 in (9)
and pf becomes a linear function of
in (9)
and pf becomes a linear function of 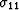 ,
, 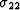 ,
,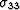 . Eliminating pf from the resulting equations, we obtain
the general expression for the strain dependence on external stress
under such confined conditions:
. Eliminating pf from the resulting equations, we obtain
the general expression for the strain dependence on external stress
under such confined conditions:
| 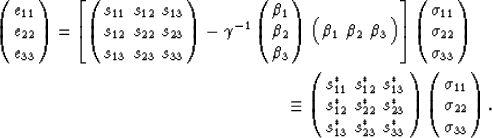 |
|
| (10) |
The sij's are fluid-drained constants, while the s*ij's are
the fluid-undrained (or fluid-confined) constants.
The fundamental result (10) was obtained earlier by both
Gassmann (1951) and Brown and Korringa (1975), and may be written
simply as
| 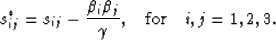 |
(11) |
This expression is just the anisotropic generalization of the
well-known Gassmann equation for isotropic, microhomogeneous
porous media.





Next: Eigenvectors for Transverse Isotropy
Up: Berryman: Poroelastic fluid effects
Previous: FLUID-SATURATED POROELASTIC ROCKS
Stanford Exploration Project
5/23/2004
![]() , while the external loading
, while the external loading ![]() is changed
and the pore-fluid pressure pf is allowed to respond as necessary and
thus equilibrate.
is changed
and the pore-fluid pressure pf is allowed to respond as necessary and
thus equilibrate.
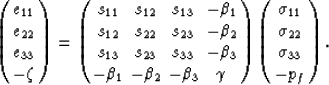
![]() in (9)
and pf becomes a linear function of
in (9)
and pf becomes a linear function of ![]() ,
, ![]() ,
,![]() . Eliminating pf from the resulting equations, we obtain
the general expression for the strain dependence on external stress
under such confined conditions:
. Eliminating pf from the resulting equations, we obtain
the general expression for the strain dependence on external stress
under such confined conditions: