




Next: About this document ...
Up: Berryman: Poroelastic fluid effects
Previous: SUMMARY AND CONCLUSIONS
-
Backus, G. E., 1962, Long-wave elastic anisotropy produced by horizontal
layering: J. Geophys. Res. 67, 4427-4440.
-
Berge, P. A., and Berryman, J. G., 1995, Realizability of negative pore
compressibility in poroelastic composites: ASME J. Appl. Mech.,
62, 1053-1062.
-
Berryman, J. G., 1999, Origin of Gassmann's equations:
Geophysics, 64, 1627-1629.
-
Berryman, J. G., 2004a, Modeling high-frequency acoustic velocities in
patchy and partially saturated porous rock using differential
effective medium theory:
SEP-112, 223-236.
-
Berryman, J. G., 2004b, Poroelastic shear modulus dependence on
pore-fluid properties arising in a model of thin isotropic layers:
Geophys. J. Int., 157, 415-425.
-
Berryman, J. G., 2004c, Seismic waves in finely layered VTI media:
Poroelasticity, Thomsen parameters, and fluid effects on shear waves:
SEP-115, 417-444.
-
Berryman, J. G., Berge, P. A., and Bonner, B. P., 2002a,
Estimating rock porosity and fluid saturation using only seismic
velocities: Geophysics 67, 391-404.
-
Berryman, J. G., Pride, S. R., and Wang. H. F., 2002b, A differential scheme
for elastic properties of rocks with dry or saturated cracks:
Geophys. J. Int., 151, 597-611.
-
Berryman, J. G., and Thigpen, L., 1985, Nonlinear and semilinear dynamic
poroelasticity with microstructure:
J. Mech. Phys. Solids, 33, 97-116.
-
Berryman, J. G., and Wang, H. F., 2001, Dispersion in poroelastic systems:
Phys. Rev. E, 64, 011303.
-
Biot, M. A., 1962, Mechanics of deformation and acoustic propagation in
porous media: J. Appl. Phys., 33, 1482-1498.
-
Biot, M. A., and Willis, D. G., 1957, The elastic coefficients of the
theory of consolidation: J. Appl. Mech., 24, 594-601.
-
Brown, R. J. S., and Korringa, J., 1975, On the dependence of the
elastic properties of a porous rock on the compressibility of a pore
fluid: Geophysics, 40, 608-616.
-
Gassmann, F., 1951, Über die elastizität poröser medien:
Veirteljahrsschrift der Naturforschenden Gesellschaft in Zürich,
96, 1-23.
-
Hudson, J. A., 1981, Wave speeds and attenuation of elastic waves in
material containing cracks: Geophys. J. R. Astr. Soc.,
64, 133-150.
-
Knight, R., and Nolen-Hoeksema, R., 1990, A laboratory study of the
dependence of elastic wave velocities on pore scale fluid distribution:
Geophys. Res. Lett., 17, 1529-1532.
-
Mavko, G., and Jizba, D., 1991, Estimating grain-scale fluid effects on
velocity dispersion in rocks: Geophysics, 56, 1940-1949.
-
Mukerji, T., and Mavko, G., 1994, Pore fluid effects on seismic velocity in
anisotropic rocks: Geophysics, 59, 233-244.
-
Murphy, William F., III, 1982, Effects of Microstructure and Pore
Fluids on the Acoustic Properties of Granular Sedimentary Materials,
Ph.D. Dissertation, Stanford University.
-
Norris, A. N., 1993, Low-frequency dispersion and attenuation in partially
saturated rocks: J. Acoust. Soc. Am., 94, 359-370.
-
O'Connell, R. J., and Budiansky, B., 1974, Seismic velocities in dry and
saturated cracked solids: J. Geophys. Res., 79, 5412-5426.
-
Rice, J. R., and Cleary, M. P., 1976, Some basic stress diffusion solutions
for fluid-saturated elastic porous media with compressible
constituents: Rev. Geophys. 14, 227-241.
-
Skempton, A. W., 1954, The pore-pressure coefficients A and B:
Geotechnique, 4, 143-147.
-
Walsh, J. B., 1969, New analysis of attenuation in partially melted rock:
J. Geophys. Res., 74, 4333-4337.
A
The equation of an ellipse centered at the origin
whose semi-major and semi-minor axes are of
lengths a and b and whose angle of rotation with respect to the
x-axis in the (x,y)-plane is 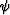 is given by
is given by
| 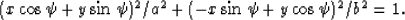 |
(35) |
For comparison, when 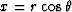 ,
, 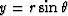 , and
a stress of magnitude
, and
a stress of magnitude 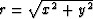 is applied
to a poroelastic system, the energy stored in the anisotropic media of
interest here [using (16) and (18)] is given by
is applied
to a poroelastic system, the energy stored in the anisotropic media of
interest here [using (16) and (18)] is given by
| ![\begin{eqnarray}
r^2f^T(\theta)\Sigma^*f(\theta) \equiv U(r,\theta) = \qquad\qqu...
...heta\sin\theta
+ 2A_{33}\sin^2\theta\right] = R^2 U(r_0,\theta).
\end{eqnarray}](img121.gif) |
|
| (36) |
In the second equation 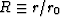 , and r0 in an
arbitrary number (say unity) having the dimensions of stress
(i.e., dimensions of Pa).
It is not hard to see that, when
, and r0 in an
arbitrary number (say unity) having the dimensions of stress
(i.e., dimensions of Pa).
It is not hard to see that, when 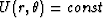 ,the two equations (35) and (36) have the same
functional form and, therefore, that contours of constant energy
in the complex (z = x +iy) plane are ellipses. Furthermore, we
can solve for the
parameters of the ellipse by setting U = 1 (in arbitrary units for now)
in (36) and then factoring r2 out of both equations. We find that
,the two equations (35) and (36) have the same
functional form and, therefore, that contours of constant energy
in the complex (z = x +iy) plane are ellipses. Furthermore, we
can solve for the
parameters of the ellipse by setting U = 1 (in arbitrary units for now)
in (36) and then factoring r2 out of both equations. We find that
| 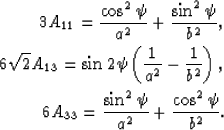 |
|
| (37) |
| |
These three equations can be inverted for the parameters of the
ellipse, giving:
| 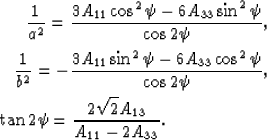 |
|
| (38) |
| |
Although contours of constant energy are of some interest, it is
probably more useful to our intuition for the poroelastic application to
think instead about contours associated with applied stresses and
strains of unit magnitude, i.e., for r = 1 (in appropriate
units) and 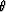 varying from to
varying from to  [again see definition
(18)]. We then have the
important function
[again see definition
(18)]. We then have the
important function 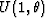 . [Note that, when
. [Note that, when 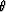 varies
instead between
varies
instead between  and
and 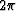 , we just get a copy of the behavior
for
, we just get a copy of the behavior
for 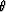 between and
between and  .The only difference is that the stress and strain vectors have an
overall minus sign relative to those on the other half-circle. For a
linear system, such an overall phase factor of unit magnitude is
irrelevant to the mechanics of the problem.] Then, if we set
.The only difference is that the stress and strain vectors have an
overall minus sign relative to those on the other half-circle. For a
linear system, such an overall phase factor of unit magnitude is
irrelevant to the mechanics of the problem.] Then, if we set
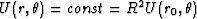 and plot
and plot 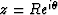 in the complex plane, we will have a plot of the ellipse of
interest with R determined analytically by
in the complex plane, we will have a plot of the ellipse of
interest with R determined analytically by
| 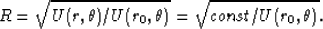 |
(39) |
We call R the magnitude of the normalized stress (i.e.,
normalized with respect to r0).
The analysis just outlined can then be repeated for the stiffness
matrix and applied strain vectors. The mathematics is completely
analogous to the case already discussed, so we will not repeat it
here. Since strain is already a dimensionless quantity, the factor
that plays the same role as r0 above can in this case be chosen
to be unity if desired, as the main purpose of the factor r0 above was
to keep track of the dimensions of the stress components.





Next: About this document ...
Up: Berryman: Poroelastic fluid effects
Previous: SUMMARY AND CONCLUSIONS
Stanford Exploration Project
5/23/2004
![]() is given by
is given by
![\begin{eqnarray}
r^2f^T(\theta)\Sigma^*f(\theta) \equiv U(r,\theta) = \qquad\qqu...
...heta\sin\theta
+ 2A_{33}\sin^2\theta\right] = R^2 U(r_0,\theta).
\end{eqnarray}](img121.gif)
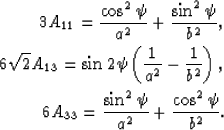
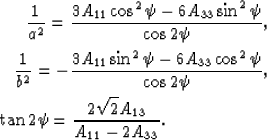
![]() varying from to
varying from to ![]() [again see definition
(18)]. We then have the
important function
[again see definition
(18)]. We then have the
important function ![]() . [Note that, when
. [Note that, when ![]() varies
instead between
varies
instead between ![]() and
and ![]() , we just get a copy of the behavior
for
, we just get a copy of the behavior
for ![]() between and
between and ![]() .The only difference is that the stress and strain vectors have an
overall minus sign relative to those on the other half-circle. For a
linear system, such an overall phase factor of unit magnitude is
irrelevant to the mechanics of the problem.] Then, if we set
.The only difference is that the stress and strain vectors have an
overall minus sign relative to those on the other half-circle. For a
linear system, such an overall phase factor of unit magnitude is
irrelevant to the mechanics of the problem.] Then, if we set
![]() and plot
and plot ![]() in the complex plane, we will have a plot of the ellipse of
interest with R determined analytically by
in the complex plane, we will have a plot of the ellipse of
interest with R determined analytically by