




Next: A look at the
Up: Alvarez et al.: Diffracted
Previous: Apex-shifted Radon Transform
As a linear transformation, the apex-shifted Radon transform can be
represented simply as
| 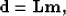 |
(1) |
where 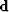 is the image in the angle domain,
is the image in the angle domain,
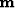 is the image in the Radon domain and
is the image in the Radon domain and
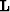 is the forward apex-shifted Radon transform operator.
To find the model
is the forward apex-shifted Radon transform operator.
To find the model 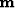 that best fits the data in a least-squares
sense, we minimize the objective function:
that best fits the data in a least-squares
sense, we minimize the objective function:
| 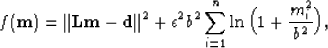 |
(2) |
where the second term is a Cauchy regularization that enforces sparseness
in the model
space. Here n is the size of the model space, and  and b are
two constants chosen a-priori:
and b are
two constants chosen a-priori:  which controls the
amount of sparseness in the model
space and b related to the minimum value below which
everything in the Radon domain should be zeroed Sava and Guitton (2003).
The least-squares inverse of
which controls the
amount of sparseness in the model
space and b related to the minimum value below which
everything in the Radon domain should be zeroed Sava and Guitton (2003).
The least-squares inverse of 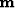 is
is
| ![\begin{displaymath}
{\bf \hat{m}} =
\left [
{\bf L'L}+\epsilon^2 {\bf diag}\Big(\frac{1}{1+\frac{m_i^2}{b^2}}\Big)
\right ]^{-1}{\bf L'd},\end{displaymath}](img11.gif) |
(3) |
where 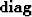 defines a diagonal operator.
Because the model space can be large, we estimate
defines a diagonal operator.
Because the model space can be large, we estimate 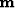 iteratively.
Notice that the objective function in Equation (2) is non-linear
because the model appears in the definition of the regularization term.
Therefore, we use a limited-memory quasi-Newton method
Guitton and Symes (2003) to find the minimum of
iteratively.
Notice that the objective function in Equation (2) is non-linear
because the model appears in the definition of the regularization term.
Therefore, we use a limited-memory quasi-Newton method
Guitton and Symes (2003) to find the minimum of 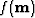 .
.





Next: A look at the
Up: Alvarez et al.: Diffracted
Previous: Apex-shifted Radon Transform
Stanford Exploration Project
5/23/2004
![\begin{displaymath}
{\bf \hat{m}} =
\left [
{\bf L'L}+\epsilon^2 {\bf diag}\Big(\frac{1}{1+\frac{m_i^2}{b^2}}\Big)
\right ]^{-1}{\bf L'd},\end{displaymath}](img11.gif)