




Next: Sparsity Constraint
Up: Alvarez et al.: Diffracted
Previous: Diffracted Multiples on ADCIGs
In order to account for the apex-shift of the diffracted
multiples (h), we define the forward and adjoint Radon transforms as a
modified version of the ``tangent-squared'' Radon transform introduced
by Biondi and Symes 2003. We define the
transformation from data space (ADCIGs) to model space
(Radon-transformed domain) as:
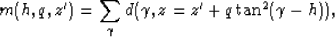
and from model space to data space as
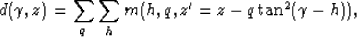
where z is depth in the data space,
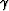 is the aperture angle, z' is the depth in the model space,
q is the moveout curvature
and h is the lateral apex shift. In this way, we transform the
two-dimensional data space of ADCIGs,
is the aperture angle, z' is the depth in the model space,
q is the moveout curvature
and h is the lateral apex shift. In this way, we transform the
two-dimensional data space of ADCIGs, 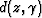 , into a three-dimensional
model space, m(z',q,h).
, into a three-dimensional
model space, m(z',q,h).
In the ideal case, primaries would be perfectly horizontal in the ADCIGs
and would thus map in the model space to the zero-curvature (q=0) plane,
i.e., a plane of dimensions depth and apex-shift distance (h,z').
Specularly-reflected multiples would map to the zero apex-shift distance
(h=0) plane, i.e., a plane of dimensions depth and curvature (q,z').
Diffracted multiples would map elsewhere in the cube depending on
their curvature and apex-shift distance.





Next: Sparsity Constraint
Up: Alvarez et al.: Diffracted
Previous: Diffracted Multiples on ADCIGs
Stanford Exploration Project
5/23/2004
![]()
![]()