Next: Discussion
Up: Flat earth synthetic
Previous: Shot-Profile Migration
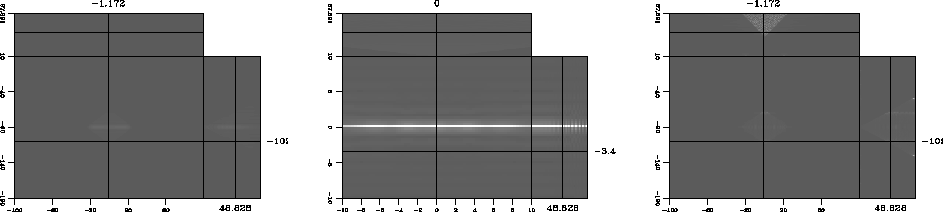
Figure 4 shows analogous plots to those presented in the
previous discussion. The same earth model and analysis
strategy is employed for these experiments, though a source-receiver
geometry for the data is employed requiring sorting the data to
midpoint-offset coordinates. The same migration split-step
Fourier migration kernel is used. While the panel a
result employs a fully populated, regular data set, the others only
used shots every 10 receiver locations. Panel b was simply
sorted and migrated. Panel c used the
same amount of live data traces as panel b, with zero traces
replacing nine out of ten traces from the full data volume. Thus, the
first and last experiments migrated the same size data cube, while
second and last experiments contain the same amount of non-trivial
data though they are an order of magnitude different in size.
Importantly, the second panel does not show the aliasing problems
present in the second panel of Figure 3 despite
the same level of shot decimation. In this experiment, the
subsampling of the shot-axis is partially mapped into both of the two
new coordinate axes before migration. The coordinate transform of
equation (1) thus distributes the axis' lower Nyquist limit
equally to the new coordinates prior to migration. Since
the output image coordinates inherit this same sampling, the
resampled data naturally adhere to the band-limiting criterion
of equation (5).
The image location and subsurface offset variables of these migrations
have the same meaning as those discussed in the shot-profile section
previously Biondi (2003). There have been two important modifications
however due to the initial coordinate transform. First, notice the
range of wavenumbers included in the second image space is drastically
limited from the panel to the left showing the migration of all
available shots. The resorting has effectively
band-limited the image space honoring the Nyquist requirement
appropriate for the image given the shot axis subsampling. Thus, the
algebraic combination of source and receiver coordinates in the
numerator makes this an inherently band-limited propagation method. Second,
the division by two of both new axes stretches their Fourier dual
domains. Notice that the alias replications in the right panel of
Figure 4 appear at a wavenumber of 20 rather than the 10 seen
in the shot-profile migration example. Despite the fact that the same number and
sampling interval for the shot axis was used in both experiments, the
division associated with the coordinate mapping has decreased the
sampling interval in the space domain and stretched energy along the
Fourier domain. This has happened independently of the three modes of
aliasing described above and needs undoing separately as well.
sg
Figure 4 Source-receiver migration
results. Left panel imaged with all data. Center panel imaged with
every tenth shot and sorted to midpoint-offset coordinates. Right
panel has zero traces inserted to fill out the decimated data set
migrated in the center panel to the data set's original size.






Next: Discussion
Up: Flat earth synthetic
Previous: Shot-Profile Migration
Stanford Exploration Project
5/23/2004