Examples

We illustrate our method with several synthetic examples of various degrees of complexity. In all examples, we use extrapolation in 2-D orthogonal Riemannian spaces (ray coordinates), and compare the results with extrapolation in Cartesian coordinates. We present images obtained by migration of synthetic datasets represented by events equally spaced in time. When we use point sources, those images are representations of Green's functions. In all examples, (x,z) are the Cartesian space coordinates, $(\t,x_0)$ are the ray coordinates for plane wave sources, and $(\t,\gamma)$ are ray coordinates for point sources. x₀ stands for surface coordinate, $\gamma$ for shooting angle, and $\t$ for one-way traveltime.

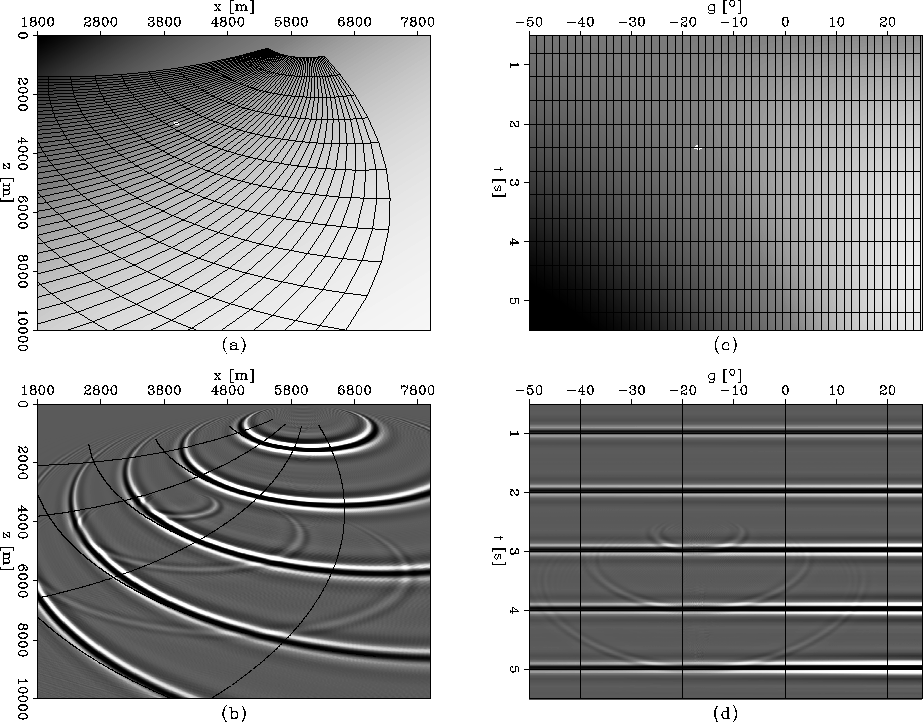
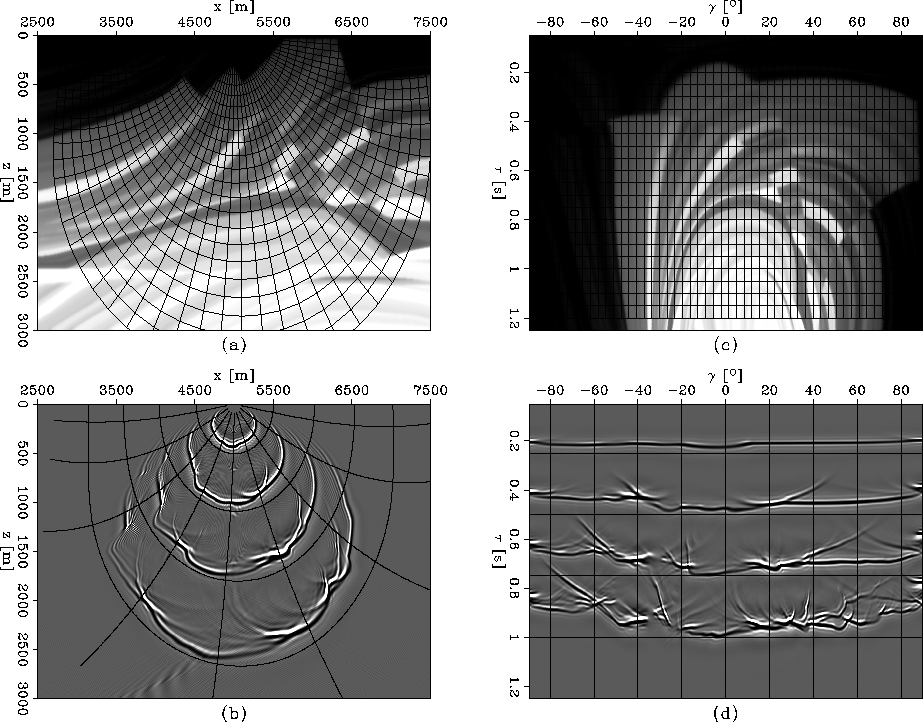
Our first example is designed to illustrate our method in a fairly simple model. We use a 2-D model with horizontal and vertical gradients $v(x,z)=250+0.2\;x+0.15\;z$ m/s which gives waves propagating from a point source a pronounced tendency to overturn (Figure 2). The model also contains a diffractor located around x=3800 m and z=3000 m.

We use ray tracing to create an orthogonal ray coordinate system corresponding to a point source on the surface at x=6000 m. Figure 2(a) shows the velocity model and the rays in the original Cartesian coordinate system (x,z). Figure 2(c) shows the velocity model mapped into the ray coordinate system ($\t,\gamma$). The diffractor is mapped to $\t=2.4$ s and $\gamma=-18^\circ$ measured from the vertical. The synthetic data we use is represented by impulses at the source location at every 0.25 s. In ray coordinates, this source is represented by a plane-wave evenly distributed over all shooting angles $\gamma$.Ideally, an image obtained by migrating such a dataset is a representation of the acoustic wavefield produced by a source which pulsates periodically.

Figure 2(b) shows the image obtained by downward continuation in Cartesian coordinates using the standard $15^\circ$ equation. Figure 2(d) shows the image obtained by wavefield extrapolation in ray coordinates using the equivalent $15^\circ$ equation. The overlays in panels (b) and (d) are wavefronts at every 0.25 s and rays shot at every $20^\circ$ to facilitate one-to-one comparisons between the images in ray and Cartesian coordinates.

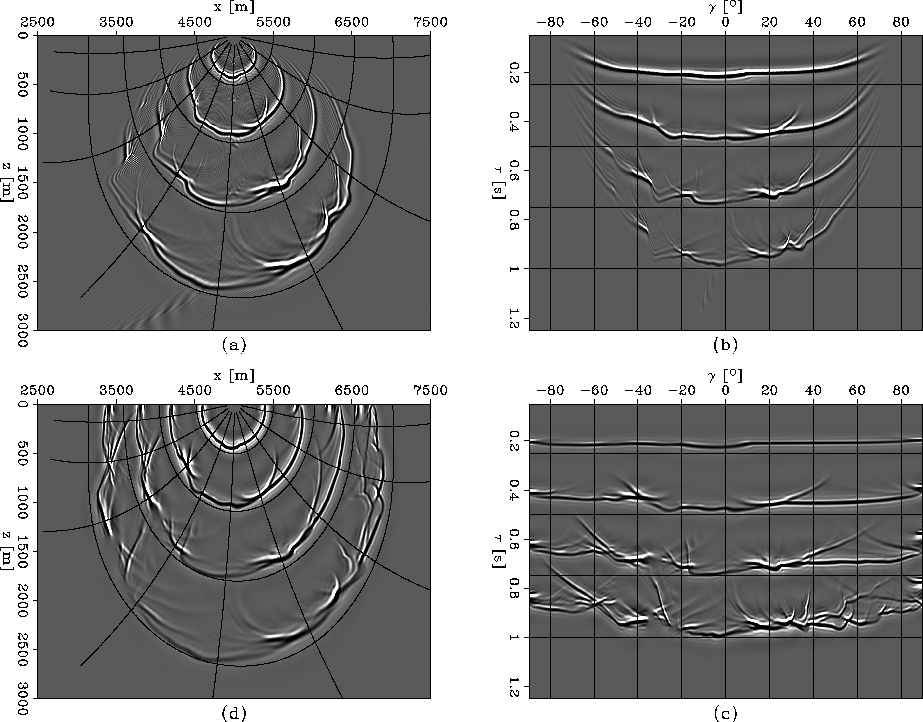
Figure 3 is a direct comparison of the results obtained by extrapolation in the two coordinate systems. The image created by extrapolation in Cartesian coordinates (a) is mapped to ray coordinates (b). The image created by extrapolation in ray coordinates (c) is mapped to Cartesian coordinates (d). Since we use the same velocity for ray tracing and for wavefield extrapolation, we expect the wavefields and the overlain wavefronts to be in agreement. The most obvious mismatch occurs in regions where the $15^\circ$ equation fails to extrapolate correctly at steep dips (around $\gamma=(-20,-50)^\circ$.This is not surprising since, as its name indicates, this equation is only accurate up to $15^\circ$.However, this limitation is eliminated in ray coordinates, because the coordinate system brings the extrapolator in a reasonable position and at a good angle, although the extrapolator uses an equation of a similar order of accuracy.

Another interesting observation in Figures 3 (a) and (d) concerns the diffractor we introduced in the velocity model. When we extrapolate in Cartesian coordinates, the diffraction is only accurate to a small angle relative to the extrapolation direction (vertical). In contrast, the diffraction develops relative to the propagation direction when computed in ray coordinates, thus being more accurate after mapping to Cartesian coordinates.

 

RCsim.com.ps
Figure 2 Simple linear gradient model: Cartesian coordinates (a,b) and ray coordinates (c,d). velocity model with an overlay of the ray coordinate system initiated by a point source at the surface (a); image obtained by downward continuation in Cartesian coordinates with the $15^\circ$ equation (b); velocity model with an overlay of the ray coordinate system (c); image obtained by wavefield extrapolation in ray coordinates with the $15^\circ$ equation (d).

 

RCsim.f15.ps
Figure 3 Simple linear gradient model: the image obtained by downward continuation in Cartesian coordinates with the $15^\circ$ equation (a); the image in panel (a) interpolated to ray coordinates (b); image obtained by extrapolation in ray coordinates with the $15^\circ$ equation (c); the image in panel (c) interpolated to Cartesian coordinates (d).

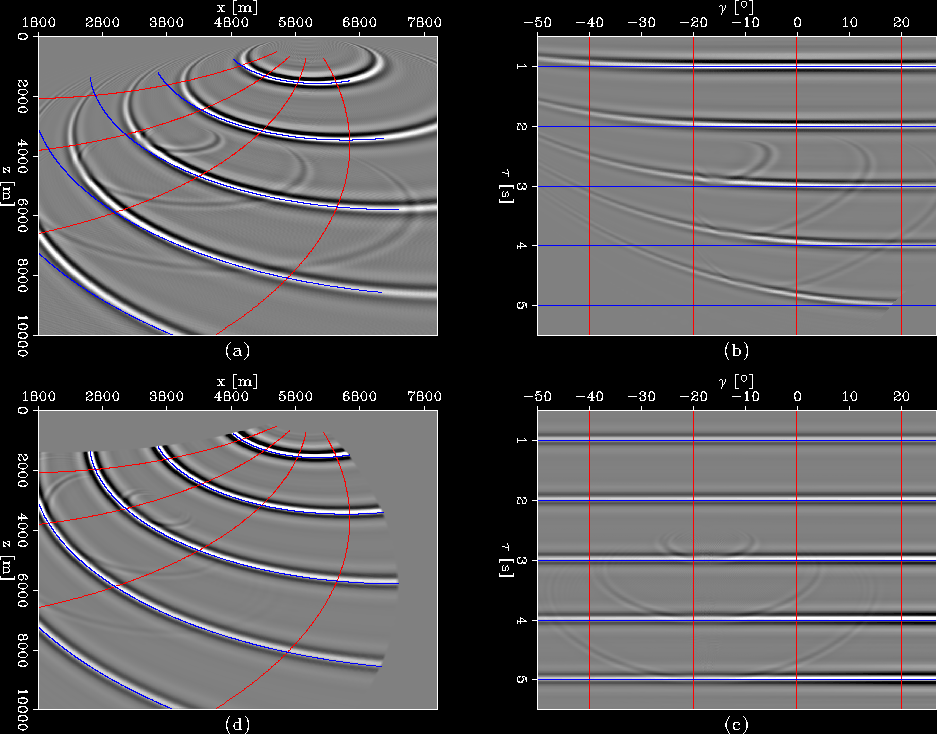We can also observe that the diffractions created by the anomaly in the velocity model are not at all limited in the ray coordinates domain. In a beam-type approach, such diffraction would not develop beyond the extent of any particular beam which interacts with it. Neighboring beams would be completely insensitive to the presence of the velocity anomaly.

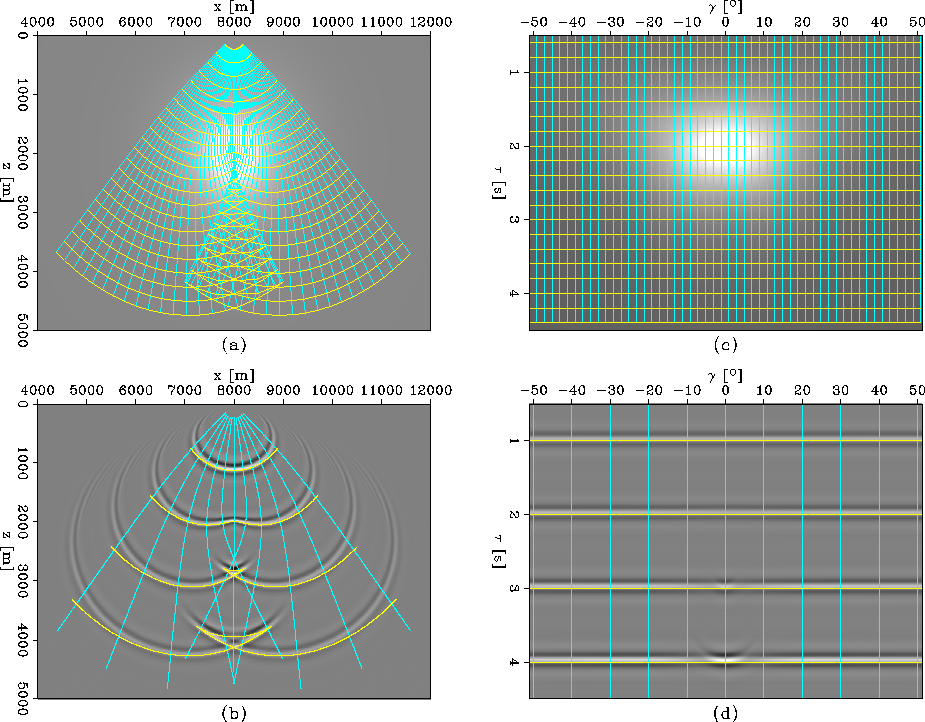
The second example concerns a smooth velocity with a negative Gaussian anomaly which creates a triplication of the ray coordinate system (Figure 4). Everything other than the velocity model is identical to its counterpart in the preceding example. Similarly to Figure 2, panels (a) and (b) correspond to Cartesian coordinates, and panels (c) and (d) correspond to ray coordinates. Using regularization of the ray coordinates parameters, we are able to extrapolate through the triplication. The small discrepancy between the wavefields and the corresponding wavefronts indicate that our method of ray tracing is not perfectly accurate in the triplicating region, and the wavefield extrapolation is correcting for the kinematic differences.

 

RCga1.com.ps
Figure 4 Gaussian anomaly model: Cartesian coordinates (a,b) and ray coordinates (c,d). velocity model with an overlay of the ray coordinate system initiated by a point source at the surface (a); image obtained by downward continuation in Cartesian coordinates with the $15^\circ$ equation (b); velocity model with an overlay of the ray coordinate system (c); image obtained by wavefield extrapolation in ray coordinates with the $15^\circ$ equation (d).

 

RCga1.f15.ps
Figure 5 Gaussian anomaly model: the image obtained by downward continuation in Cartesian coordinates with the $15^\circ$ equation (a); the image in panel (a) interpolated to ray coordinates (b); image obtained by extrapolation in ray coordinates with the $15^\circ$ equation (c); the image in panel (c) interpolated to Cartesian coordinates (d).

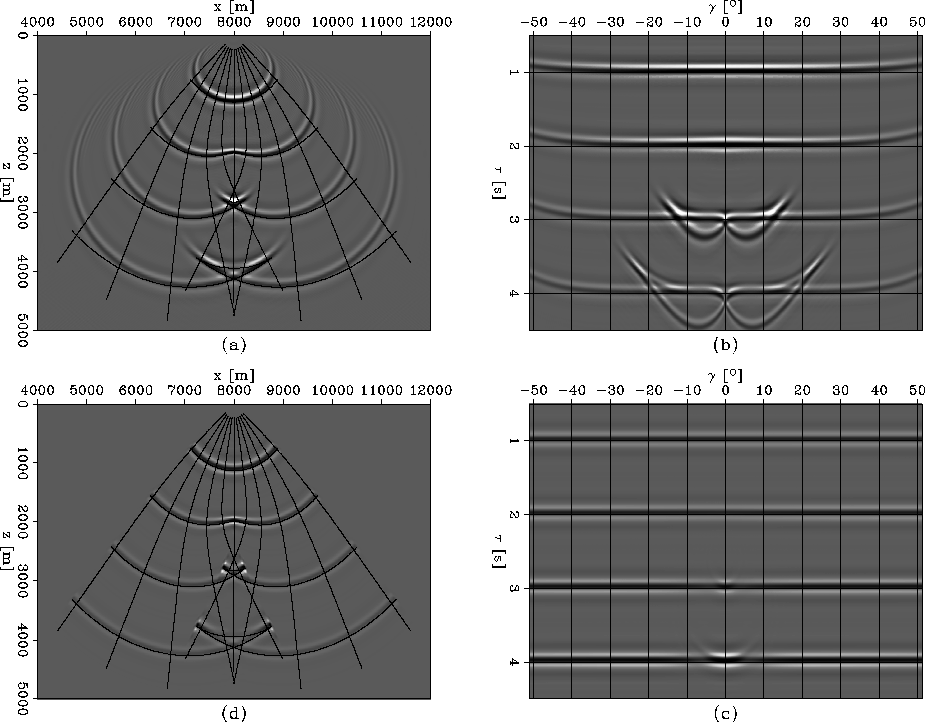Figure 5 is similar to Figure 3. The ``butterfly'' in panel (b) is another indication that the ray coordinate system is triplicating, and different shooting directions pick up the same energy from the wavefield extrapolated in Cartesian coordinates (a). None of this happens when we extrapolate in ray coordinates (c) and interpolate to Cartesian coordinates (d).

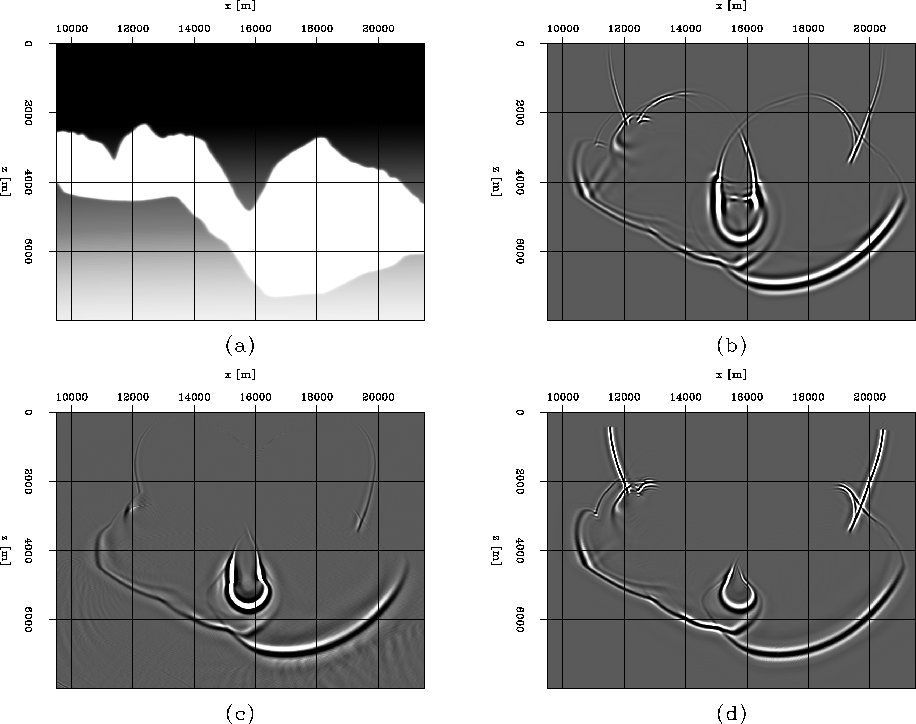
Our next example concerns the more complicated Marmousi model. Figure 6 shows the velocity models mapped into the two different domains, and the wavefields obtained by extrapolation in each one of them. We create the ray coordinate system by ray tracing in a smooth version of the model, and extrapolate in the rough version. The source is located on the surface at x=5000 m.

In this example, the wavefields triplicate in both domains (Figure 7). Since we are using a $15^\circ$ equation, extrapolation in Cartesian coordinates is only accurate for the small incidence angles, as can be seen in panels (a) and (b). In contrast, extrapolating in ray coordinates (c) does not have the same angle limitation, which can also be seen after mapping back to Cartesian coordinates (d).

 

RCma1.com.ps
Figure 6 Marmousi model: Cartesian coordinates (a,b) and ray coordinates (c,d). velocity model with an overlay of the ray coordinate system initiated by a point source at the surface (a); image obtained by downward continuation in Cartesian coordinates with the $15^\circ$ equation (b); velocity model with an overlay of the ray coordinate system (c); image obtained by wavefield extrapolation in ray coordinates with the $15^\circ$ equation (d).

 

RCma1.f15.ps
Figure 7 Marmousi model: the image obtained by downward continuation in Cartesian coordinates with the $15^\circ$ equation (a); the image in panel (a) interpolated to ray coordinates (b); image obtained by extrapolation in ray coordinates with the $15^\circ$ equation (c); the image in panel (c) interpolated to Cartesian coordinates (d).

 

RCma1.zom.ps
Figure 8 Marmousi model: Velocity model (a); image obtained by wavefield extrapolation in ray coordinates using the $15^\circ$ equation (b) and the split-step equation (c); image obtained using downward continuation in Cartesian coordinates with the $45^\circ$ equation (d), the $15^\circ$ equation (e) and the split-step equation (f).

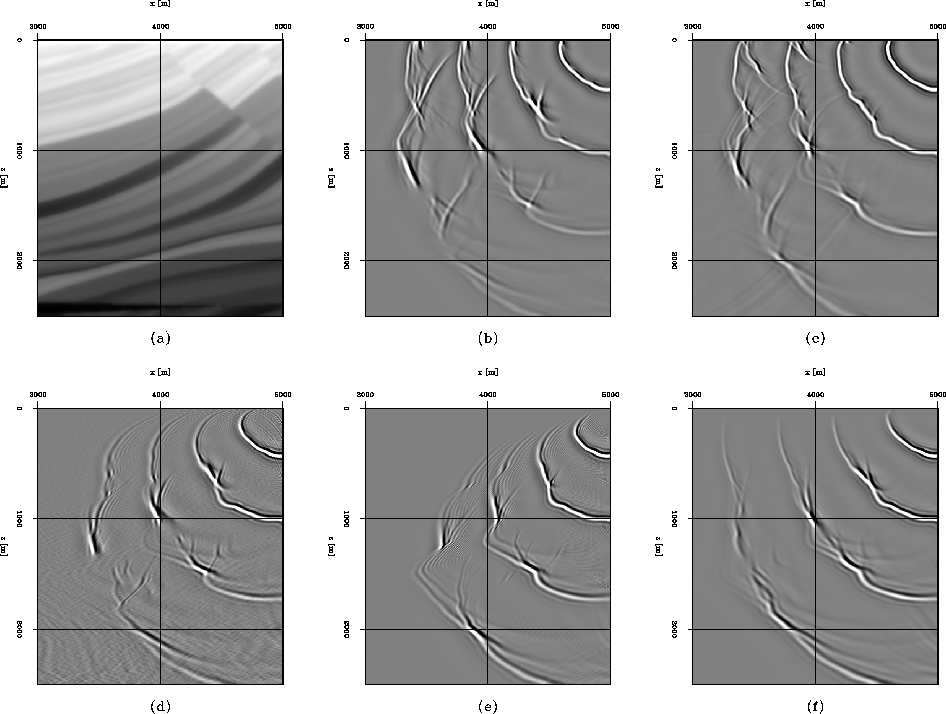
Figure 8 is a close-up comparison of the wavefields obtained by extrapolation with different methods in different domains. Panel (a) is a window of the velocity model for reference. Panels (b) and (c) are obtained by extrapolation in ray coordinates using the $15^\circ$ and split-step equations, respectively. Panels (d), (e) and (f) are obtained by downward continuation in Cartesian coordinates using the $45^\circ$, $15^\circ$ and split-step equations, respectively. The ray coordinates extrapolation results are similar to the Cartesian coordinates results in the regions where the wavefields propagate mostly vertically, but are much better in the regions where the wavefields propagate almost horizontally.

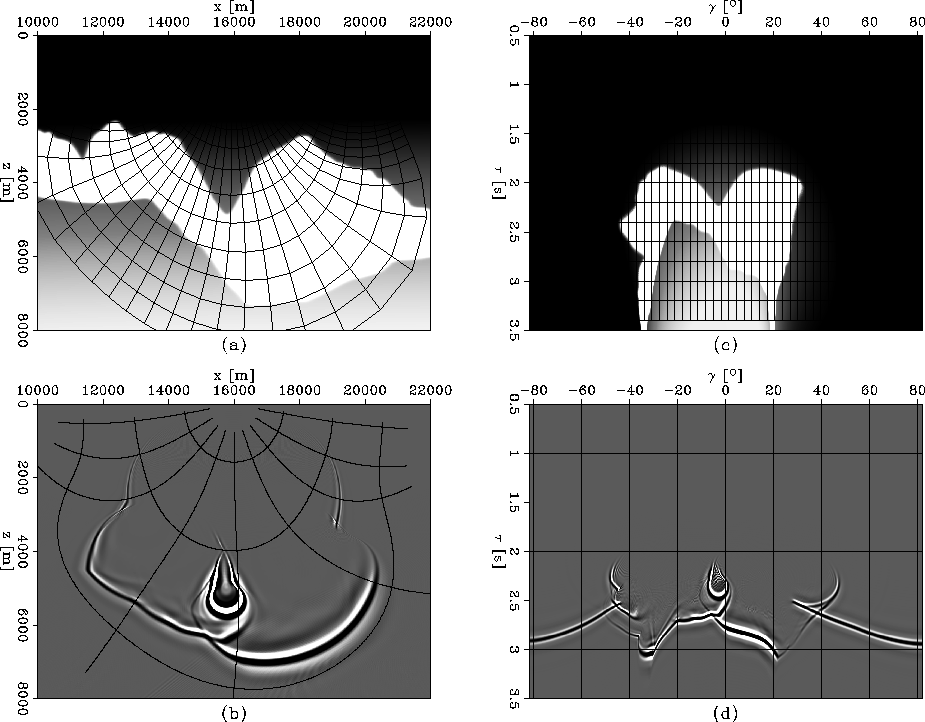
Next, we present another example in the Sigsbee 2A model. We consider two types of ray coordinates: one initiated by a plane wave at the surface (Figure 9), and one initiated by a point source at the surface at x=16000 m. (Figure 10). Similarly to the preceding examples, we observe complicated wavefield propagation, with many triplications, of the extrapolated wavefields.

 

RCzg2.com.pw
Figure 9 Sigsbee 2A model: Cartesian coordinates (a,b) and ray coordinates (c,d). velocity model with an overlay of the ray coordinate system initiated by a plane source at the surface (a); image obtained by downward continuation in Cartesian coordinates with the $15^\circ$ equation (b); velocity model with an overlay of the ray coordinate system (c); image obtained by wavefield extrapolation in ray coordinates with the $15^\circ$ equation (d).

 

RCzg2.com.ps
Figure 10 Sigsbee 2A model: Cartesian coordinates (a,b) and ray coordinates (c,d). velocity model with an overlay of the ray coordinate system initiated by a point source at the surface (a); image obtained by downward continuation in Cartesian coordinates with the $15^\circ$ equation (b); velocity model with an overlay of the ray coordinate system (c); image obtained by wavefield extrapolation in ray coordinates with the $15^\circ$ equation (d).

 

RCzg2.zom.ps
Figure 11 Sigsbee 2A model: Velocity (a); finite-difference solution to the two-way acoustic wave equation for a point source at x=16000 m (b); image obtained by downward continuation in Cartesian coordinates with the $45^\circ$ equation (c); image obtained by wavefield extrapolation in ray coordinates with the $15^\circ$ equation (d).

Figure 11 is a close-up comparison of the wavefields obtained by extrapolation with different methods in different domains. Panel (a) is a window of the velocity model for reference. Panel (b) is the wavefield obtained by finite-difference modeling using the two-way acoustic wave equation. This panel contains not only waves propagating forward, but also reflections which are not going to be modeled in the one-way extrapolation results. Panel (c) is obtained by downward continuation in Cartesian coordinates using the $45^\circ$equation, and panel (d) is obtained by extrapolation in ray coordinates using the $15^\circ$ equation. We can observe good match of the forward propagating wavefields in (b) and (d), in contrast to the poor match with panel (c) in the regions of nearly horizontal propagation.

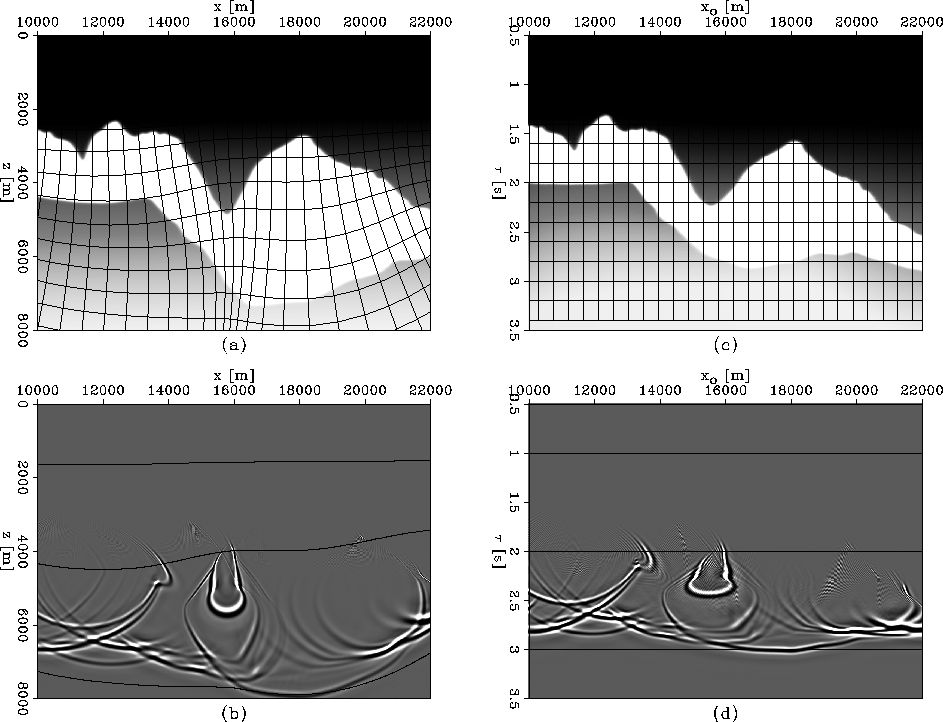
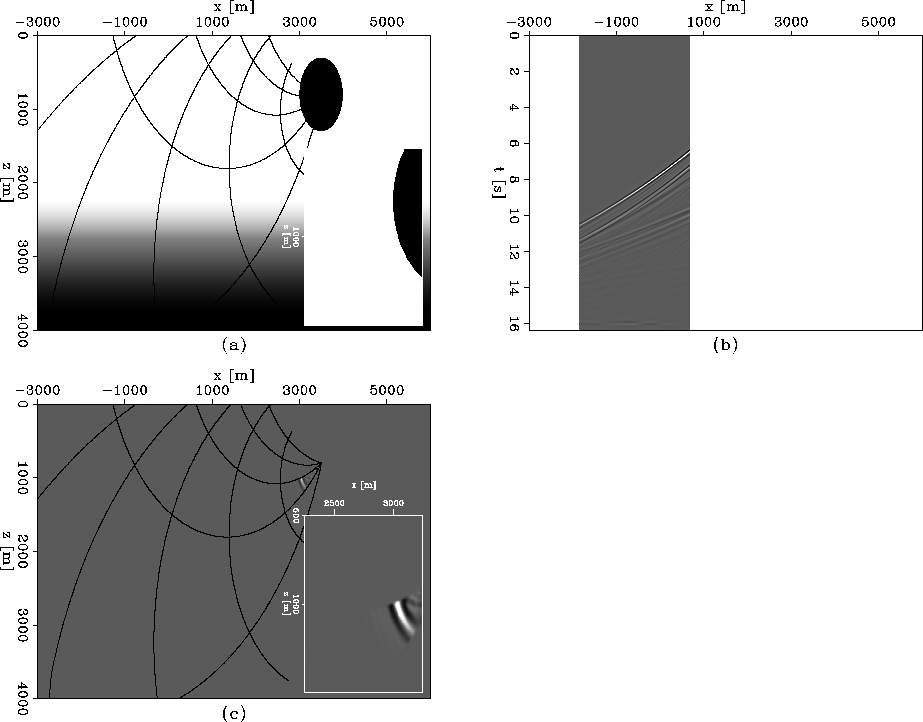
Finally, we present an example of zero-offset migration of overturning reflections using Riemannian wavefield extrapolation. Figure 12 depicts the velocity model (a), the recorded data (b), and the migrated image (c). The overlay is a sketch of the ray coordinate system used for migration. The first event in the data corresponds to the overturning reflection from the ball and is imaged correctly, and the later events are multiple reverberations inside the ball which are not imaged with our method.

 

RCba1.ovt
Figure 12 Imaging of overturning reflections using Riemannian wavefield extrapolation. Velocity model (a), zero-offset data (b), and migrated image (c).