Discussion

We have shown in the preceding section several methods that can be used to create image perturbations to be inverted for slowness perturbations:

$$\begin{eqnarray} \Delta \mathcal R_b&=& \sum_\omega\left(\mathcal U- \mathcal U_... ...r} \right\vert _{\r=\r_o} \left[\mathcal R_o\right]\; \Delta \r\;.\end{eqnarray}$$ (21) (22) (23)

Figure  shows the slowness backprojection for image perturbations computed using the definition in equation (21). From top to bottom, the panels correspond to increasing magnitudes of the slowness anomalies. In panel (a), the accumulated differences between the background and correct images is small, such that the Born approximation holds and the backprojection creates simple ``fat rays'' Woodward (1992). However, as the slowness anomaly increases, the fat rays are distorted by sign changes (b), and/or by the characteristic ellipsoidal side-lobes (c).

 

RYTOV3b.xbsbor Figure 3 Fat rays for an image perturbation defined using the Born equation (21). The slowness anomaly is gradually increasing from (a) to (c). Only the smallest anomaly is correctly handled by the Born image perturbation.

Figure  shows the slowness backprojection for image perturbations computed using the definition in equation (22). From top to bottom, the panels correspond to increasing magnitudes of the slowness anomalies. In panels (a) and (b), the accumulated phase differences between the background and correct images are small and do not wrap. Backprojection by WEMVA also creates simple undistorted fat rays. At large magnitudes, however, the phases become large enough to wrap, and backprojection from image perturbations defined by equation (22) fails (c).

 

RYTOV3b.xbsryt Figure 4 Fat rays for an image perturbation defined using the Rytov equation (22).The slowness anomaly is gradually increasing from (a) to (c). The phases are not unwrapped, thus the largest anomaly is not described correctly.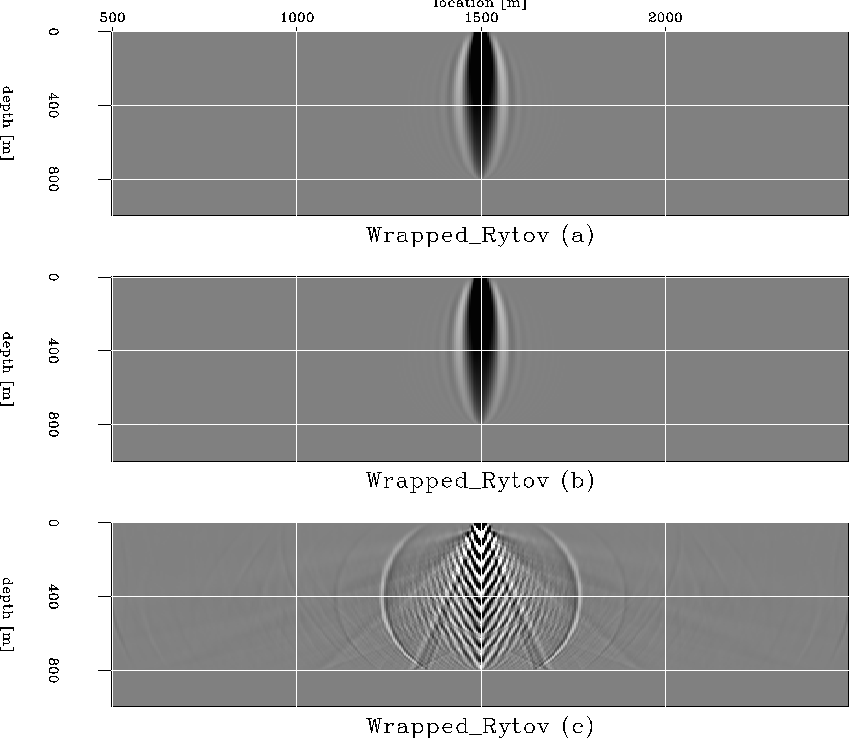

Both equation (21) and equation (22) employ the same operator for backprojection. The difference is in the method we use to define the wavefield perturbation. For equation (21) we use the difference between the complete wavefields, with the constraint of small total wavefield difference. For equation (22) we use the difference between the cumulative phases, which does not impose a constraint on the actual size of the wavefields. Thus, using equation (22), we could in principle handle arbitrarily large slowness perturbations.

However, the phases in equation (22) need to be unwrapped to obtain a meaningful wavefield differences. In complex environments, wavefields are can be quite complicated, and it is not at all trivial to estimate and unwrap their phases. Therefore, even if we could in theory use equation (22) for arbitrarily large perturbations, in practice we are constrained by our ability to unwrap the phases of complicated wavefields. Figure  shows the fat rays corresponding to the different magnitudes of slowness anomalies when the phases have been unwrapped.

 

RYTOV3b.xbsunw Figure 5 Fat rays for an image perturbation defined using the Rytov equation (22).The slowness anomaly is gradually increasing from (a) to (c). The phases are unwrapped, thus all anomalies are described correctly.

The more practical alternative we can use to create image perturbations using equation (23) is illustrated in Figure . In this case, the fat rays are not distorted at any magnitude of slowness anomaly, behavior which is similar to that of the unwrapped Rytov.

 

RYTOV3b.xbsana Figure 6 Fat rays for an image perturbation defined using the differential equation (23).The slowness anomaly is gradually increasing from (a) to (c). All anomalies are described correctly.

The explanation for this behavior lies in the definition in equation (23). The image perturbation is created by estimating the gradient of the residual migration change on the background image, followed by scaling with the appropriate $\Delta \r$ picked from a suite of images obtained with different values of the parameter $\r$.

In essence, we are using the information provided by the background image to infer the direction and magnitude of the image change. There is no limitation to how far we can go from the background image similar to the limitations of the Born and Rytov definitions. However, since we are employing a first order linearization, the accuracy of the differential image perturbation decreases with increasing $\Delta \r$.

 

dif Figure 7 A sketch of the approximations done when computing image perturbations with equation (23). In this plot, each multi-dimensional image is schematically depicted by a point. We compute a linear approximation of an image corresponding to a spatially varying $\r$ from the gradient information computed on the background image and the $\Delta \r$ picked from a suite of images. The accuracy of the linear approximation decreases with increasing $\Delta \r$.

Figure  is a schematic illustration of the transformation implied by equation (23). We can create enhanced images either by nonlinear residual migration, or by a first-order linearization around the background image. In principle, the accuracy of this approximation decreases with increasing $\Delta \r$. Therefore, in practice we cannot go arbitrarily far from any given background image and we need to run several non-linear iterations involving slowness inversion, re-migration and re-linearization.

Figure  is a summary of fat rays computed using the methods described in the preceding section. The magnitude of the slowness anomaly increases from left to right. From bottom to top we show the fat rays for the Born definition, the Rytov definition without phase unwrapping, the Rytov definition with phase unwrapping, and the differential definition.

The four panels on the left are identical, since all methods work as well for small anomalies. In the middle four panels, the fat ray obtained with the Born definition starts to break, while the Rytov (with and without phase unwrapping) and differential approaches work well. Finally, the panels on the right correspond to the highest anomaly, when only the Rytov with phase unwrapping and differential methods work.