




Next: Discussion
Up: WEMVA theory
Previous: Rytov image perturbation
Various methods can be used to improve images
created with inaccurate, reference velocity models.
Residual migration
Al-Yahya (1989); Etgen (1990); Stolt (1996)
is one such option,
although we could use other methods like
residual moveout or image continuation.
If image enhancement is done with a Stolt-type
residual migration operator 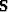 Sava (2000, 2003); Stolt (1996),
we can write a relation for
an improved image
Sava (2000, 2003); Stolt (1996),
we can write a relation for
an improved image  derived from a reference
image
derived from a reference
image 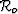
| ![\begin{displaymath}
\mathcal R= {\bf S}\left(\r \right)\left[\mathcal R_o\right]\;,\end{displaymath}](img36.gif) |
(18) |
where 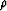 is a spatially varying scalar parameter
indicating the magnitude of residual migration
at every image point.
We can compute a linearized image perturbation by a
simple first-order expansion relative to the
parameter
is a spatially varying scalar parameter
indicating the magnitude of residual migration
at every image point.
We can compute a linearized image perturbation by a
simple first-order expansion relative to the
parameter 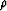
| ![\begin{displaymath}
\Delta \mathcal R_a= \left. \frac{d{\bf S}}{d\r} \right\vert _{\r=\r_o} \left[\mathcal R_o\right]\; \Delta \r\;,\end{displaymath}](img37.gif) |
(19) |
from which we can compute a wavefield perturbation 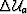 using the adjoint of the imaging operator.
using the adjoint of the imaging operator.
The operator 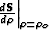 can be computed analytically, since it only depends on
the background image, while
can be computed analytically, since it only depends on
the background image, while
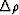 can be picked at every location
from a suite of images computed using different values
of
can be picked at every location
from a suite of images computed using different values
of 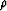 Sava and Biondi (2003).
Similar formulations are possible for other
kinds of operators (e.g., normal residual moveout),
and are not restricted to residual migration, in general,
or to Stolt residual migration, in particular.
Sava and Biondi (2003).
Similar formulations are possible for other
kinds of operators (e.g., normal residual moveout),
and are not restricted to residual migration, in general,
or to Stolt residual migration, in particular.
With this definition of the wavefield perturbation,
we can compute another slowness perturbation:
| ![\begin{displaymath}
\Delta s_a= {\bf B}^* \left(\mathcal U_o\right)\left[\Delta \mathcal U_a\right]\;.\end{displaymath}](img41.gif) |
(20) |





Next: Discussion
Up: WEMVA theory
Previous: Rytov image perturbation
Stanford Exploration Project
10/14/2003
![]() Sava (2000, 2003); Stolt (1996),
we can write a relation for
an improved image
Sava (2000, 2003); Stolt (1996),
we can write a relation for
an improved image ![]() derived from a reference
image
derived from a reference
image ![]()
![]() can be computed analytically, since it only depends on
the background image, while
can be computed analytically, since it only depends on
the background image, while
![]() can be picked at every location
from a suite of images computed using different values
of
can be picked at every location
from a suite of images computed using different values
of ![]() Sava and Biondi (2003).
Similar formulations are possible for other
kinds of operators (e.g., normal residual moveout),
and are not restricted to residual migration, in general,
or to Stolt residual migration, in particular.
Sava and Biondi (2003).
Similar formulations are possible for other
kinds of operators (e.g., normal residual moveout),
and are not restricted to residual migration, in general,
or to Stolt residual migration, in particular.