




Next: Review of Inverse Interpolation
Up: Brown: Irregular data dip
Previous: Introduction
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates a simplified conceptual model of
seismic data. Given two traces, we assume that a seismic event passes through
each trace location at times t1 and t2, and that the event takes the
form of a plane in the neighborhood of the two traces.
illustrates a simplified conceptual model of
seismic data. Given two traces, we assume that a seismic event passes through
each trace location at times t1 and t2, and that the event takes the
form of a plane in the neighborhood of the two traces.
Imagine that we wanted to measure t2-t1, given the local dip of the plane,
px and py. The total time shift is simply the sum of the time shifts
along the x and y planes, going first from x1 to x2 and then from
y1 to y2. We can write an equation directly:
|
t2-t1 = px(x2-x1) + py(y2-y1)
|
(1) |
However, in actuality we do not know px and py, but using Claerbout's
puck method, we can measure t2-t1. Implemented on a computer, the puck method
computes the time shift (in pixels) between two traces that optimally aligns a
seismic event on the two traces as a function of time. In other words, the
method measures
| 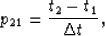 |
(2) |
where 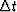 is the time sampling of the traces. We can now rewrite
equation accordingly:
is the time sampling of the traces. We can now rewrite
equation accordingly:
| 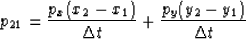 |
(3) |
Equation (3) describes the linear relationship between the computer
dip measured between traces 2 and 1, p21, and the local 3-D reflector dip.
We require two equations to obtain a unique estimate of the parameters, but the
noise and incoherency inherent to real data make it desirable to use more than
two traces and exploit the statistical ``smoothing'' of least-squares estimation.
If trace 1 is the ``master'' trace and traces 2 through n its neighbors, let
us define the forward modeling operator 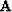
| ![\begin{displaymath}
\bold A =
\left[
\begin{array}
{cc}
\frac{x_2 - x_1}{\De...
...}{\Delta t} & \frac{y_n - y_1}{\Delta t}
\end{array}
\right]\end{displaymath}](img5.gif) |
(4) |
and the data vector 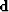
| ![\begin{displaymath}
\bold d =
\left[
\begin{array}
{c}
p_{21} \\ p_{31} \\ \vdots \\ p_{n1}
\end{array} \right].\end{displaymath}](img7.gif) |
(5) |
The estimated px and py at trace location 1 are then the solution to the
normal equations:
| ![\begin{displaymath}
\left[
\begin{array}
{c}
p_x \\ p_y
\end{array} \right] = \left( \bold A^T \bold A \right)^{-1} \bold A^T \bold d\end{displaymath}](img8.gif) |
(6) |
Inversion of the 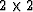 matrix
matrix 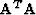 is trivial. The result
of the process is a pair of dip measurements (px and py) at each trace
location. These dip measurements must be interpolated to fill the entire model
grid. In this paper, I use an expanding-window smoothing algorithm to
accomplish the task. If reflectors are continuous, their dips should be
somewhat smooth in space, so to some extent, spatial smoothing is justified.
is trivial. The result
of the process is a pair of dip measurements (px and py) at each trace
location. These dip measurements must be interpolated to fill the entire model
grid. In this paper, I use an expanding-window smoothing algorithm to
accomplish the task. If reflectors are continuous, their dips should be
somewhat smooth in space, so to some extent, spatial smoothing is justified.





Next: Review of Inverse Interpolation
Up: Brown: Irregular data dip
Previous: Introduction
Stanford Exploration Project
10/14/2003
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrates a simplified conceptual model of
seismic data. Given two traces, we assume that a seismic event passes through
each trace location at times t1 and t2, and that the event takes the
form of a plane in the neighborhood of the two traces.
illustrates a simplified conceptual model of
seismic data. Given two traces, we assume that a seismic event passes through
each trace location at times t1 and t2, and that the event takes the
form of a plane in the neighborhood of the two traces.
![]()
![\begin{displaymath}
\bold A =
\left[
\begin{array}
{cc}
\frac{x_2 - x_1}{\De...
...}{\Delta t} & \frac{y_n - y_1}{\Delta t}
\end{array}
\right]\end{displaymath}](img5.gif)
![\begin{displaymath}
\bold d =
\left[
\begin{array}
{c}
p_{21} \\ p_{31} \\ \vdots \\ p_{n1}
\end{array} \right].\end{displaymath}](img7.gif)