Next: Irregular-geometry Dip Estimation Methodology
Up: Brown: Irregular data dip
Previous: Brown: Irregular data dip
The geometry of reflection seismic experiments rarely conforms to an idealized,
or nominal geometry. This is especially true in regions with unavoidable
surface obstructions like rivers, towns, or existing offshore oil platforms.
Such deviations from nominal geometry render many computer seismic processing
applications ineffective. It is therefore of considerable importance to 1)
accurately map irregularly-sampled seismic data onto a regular grid with
sufficient spatial resolution, and 2) to interpolate any missing trace locations
with reasonable values.
Any interpolation method fills missing traces using a prior estimate of the
missing data's spatial correlation; obtaining this correlation is often the main
challenge. When the data geometry is regular, many existing methods can resample
the data onto a finer grid. Sinc interpolation (e.g.: Bracewell (1986)) is
optimal for the regular resampling of band-limited data.
Crawley (2000) estimates a nonstationary prediction-error filter
(PEF) on regularly sampled, spatially-aliased seismic data and uses inverse
interpolation Claerbout (1999) to fill missing traces on a finer grid.
Fomel (2001) solves the same problem, but substitutes
``plane-wave-destructor'' filters, derived from estimated reflector dip, for a
PEF.
Unfortunately, irregular data geometry renders most conventional methods,
including those mentioned previously, inapplicable. To reliably estimate
autoregressive filters, like the PEF, all points in the filter stencil must, but
generally do not, fall on known data locations. A multi-scale autoregression
technique Curry and Brown (2001); Curry (2002) has yielded some
success by estimating the PEF simultaneously from data subsampled to a series of
different resolutions. Biondi and Vlad (2001) uses azimuth moveout
to transform known data to arbitrary azimuth/offset bins to constrain missing
data. Other techniques (e.g: Liu and Sacchi (2001) and
Zwartjes and Hindriks (2001)) solve an inverse interpolation problem in the
Discrete Fourier Transform domain by regularizing the unknown coefficients.
Nonetheless, a industry-standard technique does not yet exist.
In this short note, I present a different way to obtain the correlation between
irregularly-sampled traces in three dimensions. Given a pair of traces, as
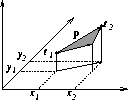
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , reflector dip can be measured along
an arbitrary azimuth, by (for instance) Claerbout's ``puck'' method
Claerbout (1992). If the dip between a master trace and two or
more neighbors is measured along two distinct azimuths, we can solve a simple
least-squares problem for the dip in the x- and y-directions at the master
trace's location. Both geology and survey geometry often dictate that the
reflector dip should vary smoothly in space. Therefore it is both natural and
intuitive to extend the estimated reflector dip to missing data locations.
, reflector dip can be measured along
an arbitrary azimuth, by (for instance) Claerbout's ``puck'' method
Claerbout (1992). If the dip between a master trace and two or
more neighbors is measured along two distinct azimuths, we can solve a simple
least-squares problem for the dip in the x- and y-directions at the master
trace's location. Both geology and survey geometry often dictate that the
reflector dip should vary smoothly in space. Therefore it is both natural and
intuitive to extend the estimated reflector dip to missing data locations.
I test my dip estimation scheme on a sparsely and irregularly sampled 3-D
synthetic model. I use the estimated dip to compute ``steering filters''
Clapp et al. (1997) which regularize an inverse interpolation problem.
This choice of regularization leads to a far better result than the spatial
gradient operator, which corresponds to the assumption of zero dip between
traces.
puck-irreg-schem
Figure 1






Next: Irregular-geometry Dip Estimation Methodology
Up: Brown: Irregular data dip
Previous: Brown: Irregular data dip
Stanford Exploration Project
10/14/2003
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , reflector dip can be measured along
an arbitrary azimuth, by (for instance) Claerbout's ``puck'' method
Claerbout (1992). If the dip between a master trace and two or
more neighbors is measured along two distinct azimuths, we can solve a simple
least-squares problem for the dip in the x- and y-directions at the master
trace's location. Both geology and survey geometry often dictate that the
reflector dip should vary smoothly in space. Therefore it is both natural and
intuitive to extend the estimated reflector dip to missing data locations.
, reflector dip can be measured along
an arbitrary azimuth, by (for instance) Claerbout's ``puck'' method
Claerbout (1992). If the dip between a master trace and two or
more neighbors is measured along two distinct azimuths, we can solve a simple
least-squares problem for the dip in the x- and y-directions at the master
trace's location. Both geology and survey geometry often dictate that the
reflector dip should vary smoothly in space. Therefore it is both natural and
intuitive to extend the estimated reflector dip to missing data locations.