




Next: Slow Waves
Up: Low Frequency Asymptotics for
Previous: Low Frequency Asymptotics for
Compressional and shear waves have almost the same asymptotic behavior
at low frequencies, but the analysis for shear waves is much shorter,
so we will present only the shear wave analysis here.
The wavenumber ks for shear wave propagation is determined by
(14), and when 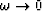 we have
we have
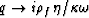 , so
, so
| ![\begin{eqnarray}
k_s^2 = {{\omega^2\rho}\over{\mu_d}}\left[1 + i{{\rho_f\kappa\omega}\over{\rho \eta}}\right].
\end{eqnarray}](img41.gif) |
(20) |
Thus, when the loss tangent is a small number, we find the shear
wave quality factor is
| 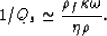 |
(21) |
Total attenuation along the path of a shear wave is then determined
by the integral 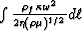 along the path of the wave. We assume for the sake of argument that
the fluid is the same throughout the reservoir. So all fluid factors
as well as frequency are constant. The solid material parameters
along the path of the wave. We assume for the sake of argument that
the fluid is the same throughout the reservoir. So all fluid factors
as well as frequency are constant. The solid material parameters
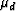 and
and 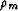 and also the porosity
and also the porosity 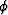 (which is hidden
in
(which is hidden
in 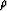 ) may vary in the reservoir, but these variations will be
treated here as negligible compared the variations in the permeability
) may vary in the reservoir, but these variations will be
treated here as negligible compared the variations in the permeability
 . Thus, we find that the total attenuation along a path of
length
. Thus, we find that the total attenuation along a path of
length 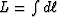 is approximately proportional to
is approximately proportional to 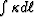 . The average attenuation per unit length of the travel path
is therefore proportional to
. The average attenuation per unit length of the travel path
is therefore proportional to 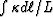 , which is just the
mean of the permeability along the wave's path. This result is also
true for the compressional waves, but the other multiplicative factors
are a bit more complicated in that case.
, which is just the
mean of the permeability along the wave's path. This result is also
true for the compressional waves, but the other multiplicative factors
are a bit more complicated in that case.





Next: Slow Waves
Up: Low Frequency Asymptotics for
Previous: Low Frequency Asymptotics for
Stanford Exploration Project
10/14/2003
![]() we have
we have
![]() , so
, so