




Next: Discussion
Up: Low Frequency Asymptotics for
Previous: Compressional and Shear Waves
In contrast, the slow compressional wave can have two very different
types of behavior at low frequency depending on the magnitude of the
permeability. The wavenumber k- for slow wave propagation is
determined by (15). To simplify this equation, we note that
it is an excellent approximation to take
| ![\begin{eqnarray}
k_-^2\simeq b + f = {{\omega^2}\over{\Delta}} \left[qH - 2\rho_f C+\rho M\right].
\end{eqnarray}](img50.gif) |
(22) |
So, at low frequencies, k-2 is proportional to q, whereas
ks2 was inversely proportional to q. Then, for small
frequencies but large values of the permeability,
![$q \to \rho_f[\alpha/\phi + i\eta/\kappa\omega]$](img51.gif) . Substituting this
into (22), we find that
. Substituting this
into (22), we find that
| ![\begin{eqnarray}
k_-^2 = {{\omega^2}\over{\Delta}} \left[\alpha\rho_f H/\phi - 2\rho_f C + \rho M + i\eta\rho_f H/\kappa\omega\right].
\end{eqnarray}](img52.gif) |
(23) |
So as 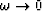 for large
for large  , there will be an intermediate
frequency regime in which the slow wave has a well-defined quality factor
, there will be an intermediate
frequency regime in which the slow wave has a well-defined quality factor
| 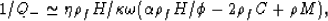 |
(24) |
which for strong frame materials reduces to
| 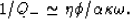 |
(25) |
Except for some factors of density, porosity, and tortuosity, this
expression is essentially the inverse of the corresponding expression
for 1/Qs. Obviously both factors cannot be small simultaneously
except for a very limited range of frequencies, which is determined
by the factor 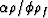 . Although
the tortuosity
. Although
the tortuosity 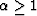 in general it can have a wide range of
values, for granular media it is typical to find
in general it can have a wide range of
values, for granular media it is typical to find 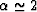 or
3. In addition,
or
3. In addition,  is also scale invariant, i.e., it
does not depend on the size of the particles composing the granular
medium. So, the presence of
is also scale invariant, i.e., it
does not depend on the size of the particles composing the granular
medium. So, the presence of  multiplying
multiplying  in
(25) does not change the fact that the slow-wave
attenuation is strongly influenced by fluctuations in the permeability
in
(25) does not change the fact that the slow-wave
attenuation is strongly influenced by fluctuations in the permeability
 . Being proportional to the square of the typical particle
sizes, the permeability is itself not scale invariant. There is
nevertheless a fairly small range of frequencies in which the
approximation in (25) is valid, say from about 20 kHz
to a few MHz for
. Being proportional to the square of the typical particle
sizes, the permeability is itself not scale invariant. There is
nevertheless a fairly small range of frequencies in which the
approximation in (25) is valid, say from about 20 kHz
to a few MHz for  's on the order of 1 D (
's on the order of 1 D (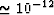 m2). This is the range where a propagating slow wave might be
expected to be seen, and in fact has been observed in laboratory
experiments (Plona, 1980).
m2). This is the range where a propagating slow wave might be
expected to be seen, and in fact has been observed in laboratory
experiments (Plona, 1980).
For still smaller permeabilities or smaller frequencies or both,
the leading approximation for the slow wave dispersion is instead given by
| 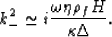 |
(26) |
This type of dispersion relation corresponds to a purely diffusive
process having a diffusion coefficient 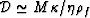 .This result follows directly from the second equation in (2)
when the porous frame is sufficiently rigid.
.This result follows directly from the second equation in (2)
when the porous frame is sufficiently rigid.
We reach the same conclusion about how fluctuating permeability
affects the propagation or diffusion of increments of fluid content
(i.e., masses of excess fluid particles) in both of these cases.
For the wave propagation situation of (25), we clearly
have, by simple analogy to the arguments given already, that the
average attenuation per unit length along the wave's path is
proportional to 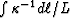 . Similarly, in the limit
of the diffusion process described by (26), then for
a planar excitation diffusing through such a system in a direction
perpendicular to the bedding planes, or for regions of isotropic
random fluctuations in permeability, we again expect the overall
effective diffusion rate to depend on the same average quantity:
. Similarly, in the limit
of the diffusion process described by (26), then for
a planar excitation diffusing through such a system in a direction
perpendicular to the bedding planes, or for regions of isotropic
random fluctuations in permeability, we again expect the overall
effective diffusion rate to depend on the same average quantity:
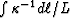 . Thus, measurements of slow waves or of
fluid increment diffusion on the macroscale will measure an effective
permeability that is largely controlled by the smallest permeability
present in the system. Clearly, this is exactly the opposite
dependence we found for the dependence of the shear wave and also
for the fast compressional wave, and must cause difficulties for
up-scaling in Biot's theory, where only one permeability parameter
is available for the fitting of data.
. Thus, measurements of slow waves or of
fluid increment diffusion on the macroscale will measure an effective
permeability that is largely controlled by the smallest permeability
present in the system. Clearly, this is exactly the opposite
dependence we found for the dependence of the shear wave and also
for the fast compressional wave, and must cause difficulties for
up-scaling in Biot's theory, where only one permeability parameter
is available for the fitting of data.





Next: Discussion
Up: Low Frequency Asymptotics for
Previous: Compressional and Shear Waves
Stanford Exploration Project
10/14/2003
![]() . Similarly, in the limit
of the diffusion process described by (26), then for
a planar excitation diffusing through such a system in a direction
perpendicular to the bedding planes, or for regions of isotropic
random fluctuations in permeability, we again expect the overall
effective diffusion rate to depend on the same average quantity:
. Similarly, in the limit
of the diffusion process described by (26), then for
a planar excitation diffusing through such a system in a direction
perpendicular to the bedding planes, or for regions of isotropic
random fluctuations in permeability, we again expect the overall
effective diffusion rate to depend on the same average quantity:
![]() . Thus, measurements of slow waves or of
fluid increment diffusion on the macroscale will measure an effective
permeability that is largely controlled by the smallest permeability
present in the system. Clearly, this is exactly the opposite
dependence we found for the dependence of the shear wave and also
for the fast compressional wave, and must cause difficulties for
up-scaling in Biot's theory, where only one permeability parameter
is available for the fitting of data.
. Thus, measurements of slow waves or of
fluid increment diffusion on the macroscale will measure an effective
permeability that is largely controlled by the smallest permeability
present in the system. Clearly, this is exactly the opposite
dependence we found for the dependence of the shear wave and also
for the fast compressional wave, and must cause difficulties for
up-scaling in Biot's theory, where only one permeability parameter
is available for the fitting of data.