




Next: Low Frequency Asymptotics for
Up: Berryman: Scale-up in poroelastic
Previous: INTRODUCTION
For long-wavelength disturbances (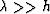 , where h is a
typical pore size) propagating through a single-porosity porous
medium, we define average values of the (local) displacements in the
solid and also in the saturating fluid. The average displacement
vector for the solid
frame is
, where h is a
typical pore size) propagating through a single-porosity porous
medium, we define average values of the (local) displacements in the
solid and also in the saturating fluid. The average displacement
vector for the solid
frame is 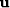 , while that for the pore fluid
is
, while that for the pore fluid
is 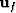 . The average displacement of the fluid relative to
the frame is
. The average displacement of the fluid relative to
the frame is 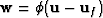 . For small
strains, the frame dilatation is e, while the increment of fluid
content is defined by
. For small
strains, the frame dilatation is e, while the increment of fluid
content is defined by
| 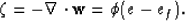 |
(1) |
With time dependence of the form 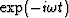 , the coupled wave
equations that follow
in the presence of dissipation are
, the coupled wave
equations that follow
in the presence of dissipation are
| 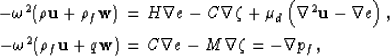 |
|
| (2) |
where 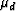 is the drained shear modulus, H, C, and M are bulk moduli,
is the drained shear modulus, H, C, and M are bulk moduli,
| 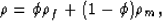 |
(3) |
and
| ![\begin{eqnarray}
q = \rho_f\left[\alpha/\phi + iF(\xi)\eta/\kappa\omega\right].
\end{eqnarray}](img10.gif) |
(4) |
The kinematic viscosity of the liquid is  ;the permeability of the porous frame is
;the permeability of the porous frame is  ;the dynamic viscosity factor is given approximately [or see
Johnson et al. (1987) for more discussion], for our choice of sign
for the frequency dependence, by
;the dynamic viscosity factor is given approximately [or see
Johnson et al. (1987) for more discussion], for our choice of sign
for the frequency dependence, by
| ![\begin{eqnarray}
F(\xi) = {\textstyle {{1}\over{4}}}
\{\xi T(\xi)/[1+2T(\xi)/i\xi]\},
\end{eqnarray}](img13.gif) |
(5) |
where
| 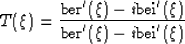 |
(6) |
and
| 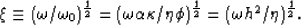 |
(7) |
The functions 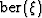 and
and 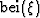 are the real and
imaginary parts of the Kelvin function. The dynamic parameter h
is a characteristic length generally associated with and comparable in
magnitude to the steady-flow hydraulic radius. The tortuosity
are the real and
imaginary parts of the Kelvin function. The dynamic parameter h
is a characteristic length generally associated with and comparable in
magnitude to the steady-flow hydraulic radius. The tortuosity
 is a pure number related to the frame inertia which has
been measured (Johnson et al., 1982)
and has also been estimated theoretically (Berryman, 1980a; 1983a).
is a pure number related to the frame inertia which has
been measured (Johnson et al., 1982)
and has also been estimated theoretically (Berryman, 1980a; 1983a).
The coefficients H, C, and M are given by
(Gassmann, 1951; Geertsma, 1957; Biot and Willis, 1957;
Geertsma and Schmidt, 1961; Stoll, 1974)
| 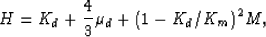 |
(8) |
| <I>CI> = (1-<I>KI><I>dI>/<I>KI><I>mI>)<I>MI>, |
|
|
(9) |
where
| ![\begin{eqnarray}
M = 1/[(1-\phi-K_d/K_m)/K_m + \phi/K_f].
\end{eqnarray}](img20.gif) |
(10) |
The constants are drained bulk and shear moduli Kd and 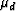 ,mineral bulk modulus Km, and fluid bulk modulus Kf.
Korringa (1981) showed equations (8)-(10) to be
correct as long as the porous material may be considered homogeneous
on the microscopic scale as well as the macroscopic scale. Also,
see a recent tutorial on Gassmann's equations (Gassmann, 1951)
by Berryman (1999).
,mineral bulk modulus Km, and fluid bulk modulus Kf.
Korringa (1981) showed equations (8)-(10) to be
correct as long as the porous material may be considered homogeneous
on the microscopic scale as well as the macroscopic scale. Also,
see a recent tutorial on Gassmann's equations (Gassmann, 1951)
by Berryman (1999).
To decouple the wave equations (2) into Helmholtz equations for
the three modes of propagation, we note that the displacements
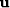 and
and 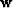 can be decomposed as
can be decomposed as
|  |
(11) |
where 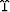 ,
, 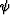 are scalar potentials and
are scalar potentials and
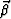 ,
, 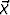 are vector potentials. Substituting
(11) into (2), we find (2) is satisfied
if two pairs of equations are satisfied:
are vector potentials. Substituting
(11) into (2), we find (2) is satisfied
if two pairs of equations are satisfied:
| 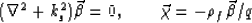 |
(12) |
and
| 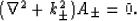 |
(13) |
The wavenumbers in (12) and (13) are defined by
| 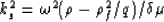 |
(14) |
and
| ![\begin{eqnarray}
k_\pm^2 = {\textstyle {{1}\over{2}}}\left[b + f \mp
\left[(b-f)^2 + 4cd \right]^{1\over2}\right],
\end{eqnarray}](img30.gif) |
(15) |
| 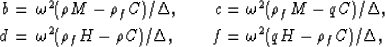 |
|
| (16) |
with
| 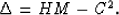 |
(17) |
The linear combination of scalar potentials has been chosen to be
| 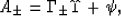 |
(18) |
where
| 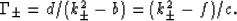 |
(19) |
With the identification (19), the decoupling is complete.
Figure 1:
Thin layering of isotropic materials produces an effective
transversely isotropic medium at low frequencies of propagation.
Overall permeability 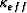 normal to the layering depends
most strongly on the most impermeable layers since
normal to the layering depends
most strongly on the most impermeable layers since
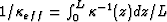 , being the harmonic mean.
In contrast, the seismic attenuation (in the usual band from 1-100 Hz)
ordinarily depends most strongly on the ones that are most permeable,
since
, being the harmonic mean.
In contrast, the seismic attenuation (in the usual band from 1-100 Hz)
ordinarily depends most strongly on the ones that are most permeable,
since 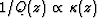 . The character of this relationship
between attenuation and permeability changes significantly
at higher frequencies as described in the text.
. The character of this relationship
between attenuation and permeability changes significantly
at higher frequencies as described in the text.
 |





Next: Low Frequency Asymptotics for
Up: Berryman: Scale-up in poroelastic
Previous: INTRODUCTION
Stanford Exploration Project
10/14/2003
![]() , where h is a
typical pore size) propagating through a single-porosity porous
medium, we define average values of the (local) displacements in the
solid and also in the saturating fluid. The average displacement
vector for the solid
frame is
, where h is a
typical pore size) propagating through a single-porosity porous
medium, we define average values of the (local) displacements in the
solid and also in the saturating fluid. The average displacement
vector for the solid
frame is ![]() , while that for the pore fluid
is
, while that for the pore fluid
is ![]() . The average displacement of the fluid relative to
the frame is
. The average displacement of the fluid relative to
the frame is ![]() . For small
strains, the frame dilatation is e, while the increment of fluid
content is defined by
. For small
strains, the frame dilatation is e, while the increment of fluid
content is defined by
![]() , the coupled wave
equations that follow
in the presence of dissipation are
, the coupled wave
equations that follow
in the presence of dissipation are
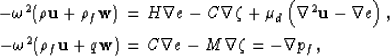
![]() and
and ![]() can be decomposed as
can be decomposed as
