




Next: THOMSEN PARAMETERS AND
Up: NOTATION AND SOME PRIOR
Previous: Gassmann results for isotropic
Backus (1962) presented an elegant method of producing the
effective constants for a thinly layered medium composed of
either isotropic or anisotropic elastic layers.
This method applies either to spatially periodic layering
or to random layering, by which we mean either that the material constants
change in a nonperiodic (unpredictable) manner from layer to layer
or that the layer thicknesses might also be random.
For simplicity, we will assume that the physical properties of the
individual layers are isotropic.
The key idea presented by Backus is that these equations
can be rearranged into a form where rapidly varying coefficients
multiply slowly varying stresses or strains.
The derivation has been given many places including Schoenberg and
Muir (1989) and Berryman (1999a). One illuminating derivation
given recently by Milton (2002) will be followed here, with the main
difference being that we assume the layering direction is
z or 3. We break the equation down into 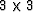 pieces so
that
pieces so
that
| 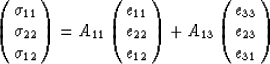 |
(8) |
and
| 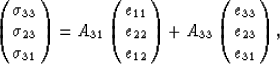 |
(9) |
where the 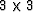 matrices are
matrices are
| 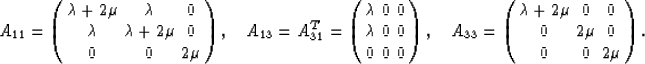 |
(10) |
Noting that the variables  ,
, 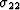 ,
, 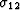 ,e33, e23, and e31 are fast variables in the layers, and
all the remaining variables are slow (actually constant), it is
advantageous to rearrange these equations so the slow variables
multiply the elastic parameter matrices and are all
on one side of the equations, while the fast variables are all alone
on the other side of the equations. Then, it is trivial to perform
the layer averages, since they depend only on the (assumed known)
values of the elastic parameters in the layers and are multiplied
by constants. Having done this, we can then transform
back into the standard forms of (8) and
(9) with the stresses and strains now reinterpreted
as the overall values, and find the following relationships
(where the star indicates the effective property of the layered
system):
,e33, e23, and e31 are fast variables in the layers, and
all the remaining variables are slow (actually constant), it is
advantageous to rearrange these equations so the slow variables
multiply the elastic parameter matrices and are all
on one side of the equations, while the fast variables are all alone
on the other side of the equations. Then, it is trivial to perform
the layer averages, since they depend only on the (assumed known)
values of the elastic parameters in the layers and are multiplied
by constants. Having done this, we can then transform
back into the standard forms of (8) and
(9) with the stresses and strains now reinterpreted
as the overall values, and find the following relationships
(where the star indicates the effective property of the layered
system):
| 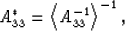 |
(11) |
| 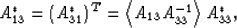 |
(12) |
and
| 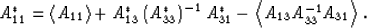 |
(13) |
The brackets 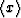 indicate the volume (or equivalaently
the one-dimensional layer) average of the quantity x in the simple
layered medium under consideration.
It follows that
the anisotropy coefficients in equation (1) are then
related to the layer parameters by the following expressions:
indicate the volume (or equivalaently
the one-dimensional layer) average of the quantity x in the simple
layered medium under consideration.
It follows that
the anisotropy coefficients in equation (1) are then
related to the layer parameters by the following expressions:
| 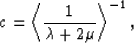 |
(14) |
| 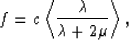 |
(15) |
| 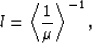 |
(16) |
| 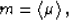 |
(17) |
| 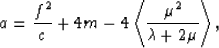 |
(18) |
and
| <I>bI> = <I>aI> - 2<I>mI>. |
|
|
(19) |
When the layering is fully periodic, these results may be attributed
to Bruggeman (1937) and Postma (1955), while for more general
layered media including random media they should be attributed to
Backus (1962).
The constraints on the Lamé parameters 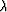 and
and 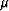 for each
individual layer are
for each
individual layer are 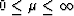 and
and
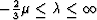 . Although, for physically stable
materials,
. Although, for physically stable
materials, 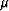 and the bulk modulus
and the bulk modulus
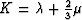 must both be nonnegative,
must both be nonnegative, 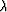 (and
also Poisson's ratio) may be negative. Large fluctuations in
(and
also Poisson's ratio) may be negative. Large fluctuations in 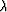 for different layers are therefore entirely possible, in principle,
but may or may not be an issue for any given region of the earth.
for different layers are therefore entirely possible, in principle,
but may or may not be an issue for any given region of the earth.
One very important fact that is known about these equations
(Backus, 1962) is that they reduce to isotropic results with
a=c, b=f, and l=m, if the shear modulus is a constant (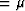 ),
regardless of the behavior of
),
regardless of the behavior of 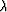 .This fact is also very important for applications involving partial
and/or patchy saturation (Mavko et al., 1998; Johnson, 2001).
Furthermore, it is closely related to the well-known bulk modulus
formula of Hill (1963) for isotropic composites having uniform shear
modulus, and also to the Hashin-Shtrikman bounds (Hashin and Shtrikman, 1961).
.This fact is also very important for applications involving partial
and/or patchy saturation (Mavko et al., 1998; Johnson, 2001).
Furthermore, it is closely related to the well-known bulk modulus
formula of Hill (1963) for isotropic composites having uniform shear
modulus, and also to the Hashin-Shtrikman bounds (Hashin and Shtrikman, 1961).





Next: THOMSEN PARAMETERS AND
Up: NOTATION AND SOME PRIOR
Previous: Gassmann results for isotropic
Stanford Exploration Project
10/16/2003
![]() pieces so
that
pieces so
that
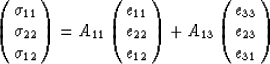
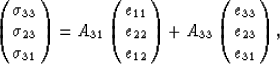
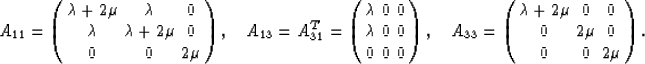
![]() ),
regardless of the behavior of
),
regardless of the behavior of ![]() .This fact is also very important for applications involving partial
and/or patchy saturation (Mavko et al., 1998; Johnson, 2001).
Furthermore, it is closely related to the well-known bulk modulus
formula of Hill (1963) for isotropic composites having uniform shear
modulus, and also to the Hashin-Shtrikman bounds (Hashin and Shtrikman, 1961).
.This fact is also very important for applications involving partial
and/or patchy saturation (Mavko et al., 1998; Johnson, 2001).
Furthermore, it is closely related to the well-known bulk modulus
formula of Hill (1963) for isotropic composites having uniform shear
modulus, and also to the Hashin-Shtrikman bounds (Hashin and Shtrikman, 1961).