




Next: Gassmann results for isotropic
Up: NOTATION AND SOME PRIOR
Previous: NOTATION AND SOME PRIOR
We begin by recalling some notation needed in the remainder of the paper.
For transversely isotropic media with vertical symmetry axis,
the relationship between components of stress 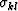 and strain
and strain
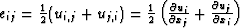 (where uj is the
jth component of the displacement vector) is given by
(where uj is the
jth component of the displacement vector) is given by
| 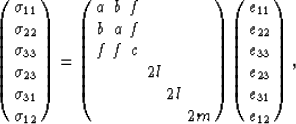 |
(1) |
where a = b + 2m (e.g., Musgrave, 1970; Auld, 1973),
with i,j,k,l obviously each ranging from 1 to 3 in Cartesian coordinates.
The matrix describes isotropic media in the special case when
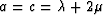 ,
, 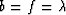 , and
, and 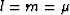 .
.
The Thomsen (1986) parameters  ,
, 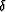 , and
, and 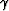 are related
to these stiffnesses by
are related
to these stiffnesses by
| 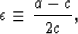 |
(2) |
| 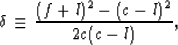 |
(3) |
| 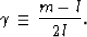 |
(4) |
For P-wave propagation in the earth near the vertical, the important
anisotropy parameter is 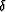 . For SV-wave propagation near the
vertical, the combination
. For SV-wave propagation near the
vertical, the combination 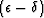 plays essentially the
same role as
plays essentially the
same role as 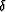 does for P-waves. For SH-waves, the pertinent
anisotropy parameter is
does for P-waves. For SH-waves, the pertinent
anisotropy parameter is 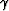 . All three of the Thomsen parameters
vanish for an isotropic medium.
. All three of the Thomsen parameters
vanish for an isotropic medium.
It is also useful to note for later reference that
| 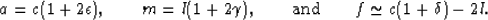 |
(5) |
In TI media, c and l are the velocities normal to the layering.
Then,  ,
, 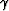 , and
, and 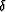 measure the deviations from
these normal velocities at other angles. We present the relevant
details of the phase velocity analysis later in the paper.
measure the deviations from
these normal velocities at other angles. We present the relevant
details of the phase velocity analysis later in the paper.





Next: Gassmann results for isotropic
Up: NOTATION AND SOME PRIOR
Previous: NOTATION AND SOME PRIOR
Stanford Exploration Project
10/16/2003
![]() and strain
and strain
![]() (where uj is the
jth component of the displacement vector) is given by
(where uj is the
jth component of the displacement vector) is given by
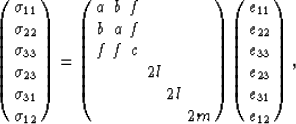
![]() ,
, ![]() , and
, and ![]() are related
to these stiffnesses by
are related
to these stiffnesses by