Determining the azimuthal range

It is often useful to limit the azimuthal range of the image. Given the strong dependence of the azimuthal resolution with aperture angle, it is natural to make the bounds of the azimuthal range functions of the aperture angle $\gamma$.Any smooth function of $\gamma$is probably adequate to define the azimuthal boundaries. I decided to apply a trigonometric function to transition between the limits at normal incidence and the limits at 90 degrees. If $\gamma_{\rm max}$ is the maximum aperture angle, $\phi_{\rm min}^0$and $\phi_{\rm max}^0$are respectively the minimum and maximum azimuth angles for $\gamma=0$ degrees, and $\phi_{\rm min}^{90}$and $\phi_{\rm max}^{90}$are respectively the minimum and maximum azimuth angles for $\gamma=90$ degrees, then I set the azimuthal limits $\phi_{\rm min}^{\gamma}$,$\phi_{\rm max}^{\gamma}$,by applying the following expressions:

$$\begin{eqnarray} \phi_{\rm min}^{\gamma} &=& \phi_{\rm min}^{90} + \left( \phi_{... ...) \left[ \sin \left( \frac { 90-\gamma } { 90 } \right) \right]^p,\end{eqnarray}$$ (1) (2)

where p is a free parameter that determines the shape of the azimuthal window.

Figure  is a generalization of Figure . The red (darker in gray scale) dots are the same as in Figure , and represent the mapping into angle domain with $\phi_{\rm min}^0=\phi_{\rm min}^{90}=-30$ degrees, and $\phi_{\rm max}^0=\phi_{\rm max}^{90}=30$ degrees. The green (lighter in gray scale) is the mapping when the azimuthal range is broader close to normal incidence, that is with $\phi_{\rm min}^0=-90$ degrees, and $\phi_{\rm max}^0=90$ degrees, and p=3. Notice that the integration domain represented by the green dots (lighter in gray scale) does not shrink close to the origin, as the original integration domain does.

Figure  shows the effect of the variable azimuthal range on the synthetic data set. Figure b shows the same ADCIG as in Figure b. The azimuthal range was constant over $\gamma$;that is $\phi_{\rm min}^0=\phi_{\rm min}^{90}=-60$ degrees, and $\phi_{\rm max}^0=\phi_{\rm max}^{90}=60$ degrees. Figure a shows the ADCIG extracted at the same location as the one in Figure b, but obtained with variable azimuthal range. The parameters were $\phi_{\rm min}^0=-60$ degrees, $\phi_{\rm min}^{90}=-5$ degrees, $\phi_{\rm max}^{90}=25$ degrees, $\phi_{\rm max}^0=60$ degrees, and p=3. The reduction in the azimuthal range attenuates the numerical noise in the image. In particular, it attenuates the ``frowning'' artifacts that, as I discussed in the previous section, are related to the narrow azimuthal coverage of the data.

Figure  shows a depth slice extracted from the image at the same depth as the slices shown in Figures -, but with the variable azimuthal range defined by the parameters listed above. The comparison of Figure  with Figure  demonstrates that the window defined using the relationships (1) and (2) preserves the coherent energy of the event, while removing noise.

 

kh_plane_wide Figure 9 Graphical representation of the effects of the variable azimuthal range on the mapping from the offset wavenumber 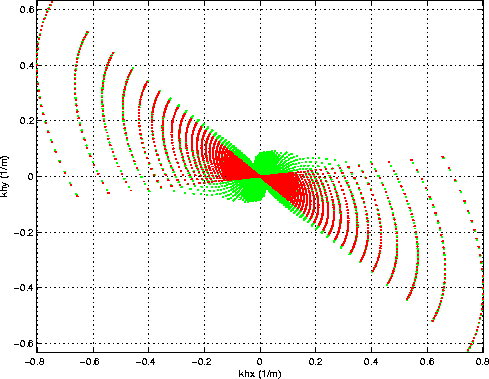$\left(k_{x_h},k_{y_h}\right)$ plane into the $\left(\gamma,\phi\right)$ plane. The green (lighter in gray scale) dots correspond to the mapping with variable azimuthal range.

 

cig-3-data6 Figure 10 ADCIGs for a synthetic data set. Left: Image obtained after application of both the angular dependent weighting and the variable azimuthal range. Right: Image obtained after application of the angular dependent weighting.

 

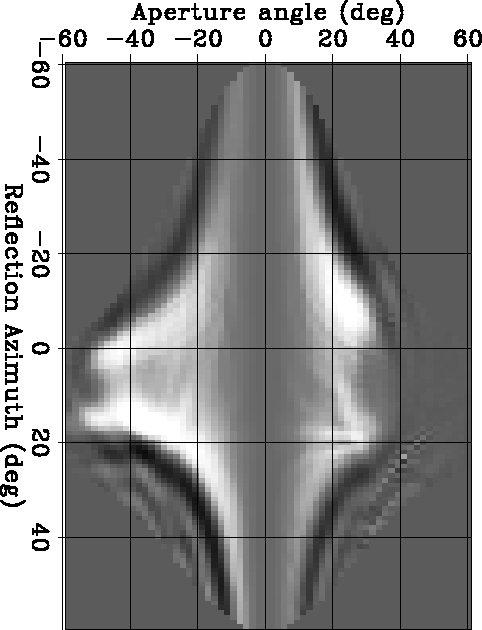
zaz-60-60-dense-all-jac-bound-v3-data6 Figure 11 Depth slice taken at the same depth as the slice shown in Figure  (z=1,1140 meters), after application of both the angular dependent weighting and the variable azimuthal range.