![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a graphical
representation of the mapping to angle domain,
and thus it illustrates the problem that I am addressing in this
paper more intuitively than the formulas.
The figure shows a uniformly sampled Cartesian grid
in the
shows a graphical
representation of the mapping to angle domain,
and thus it illustrates the problem that I am addressing in this
paper more intuitively than the formulas.
The figure shows a uniformly sampled Cartesian grid
in the
Appendix A provides the analytical form
of this transformation.
The analytical form
is fairly intricate and not easy to interpret
because the
reflection azimuth ![]() enters only indirectly as a parameter for
rotating the midpoint and offset wavenumbers.
Figure
enters only indirectly as a parameter for
rotating the midpoint and offset wavenumbers.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows a graphical
representation of the mapping to angle domain,
and thus it illustrates the problem that I am addressing in this
paper more intuitively than the formulas.
The figure shows a uniformly sampled Cartesian grid
in the
shows a graphical
representation of the mapping to angle domain,
and thus it illustrates the problem that I am addressing in this
paper more intuitively than the formulas.
The figure shows a uniformly sampled Cartesian grid
in the ![]() domain
mapped into the
domain
mapped into the ![]() plane.
Each dot corresponds to one value of
plane.
Each dot corresponds to one value of
![]() and
and ![]() ,for fixed kz, kxm and kym.
The ranges for
,for fixed kz, kxm and kym.
The ranges for
![]() and
and ![]() are:
are: ![]() and
and ![]() .The dots are densely clustered close to the origin
(corresponding to small values of
.The dots are densely clustered close to the origin
(corresponding to small values of ![]() ),
and become sparse away from the origin
(corresponding to large values of
),
and become sparse away from the origin
(corresponding to large values of ![]() ).
If this strong variability in the mapping density
were not taken into account when
a summation is performed in the angle domain,
the summation would result in a strongly distorted image.
).
If this strong variability in the mapping density
were not taken into account when
a summation is performed in the angle domain,
the summation would result in a strongly distorted image.
In this paper I consider the effects of averaging the image over reflection azimuth because it is the most challenging and interesting situation, as we will see briefly. However, similar considerations are needed when summing over aperture angles (for example when computing the ``stacked'' image after the application of a residual moveout correction to improve reflectors' coherency).
|
cig-1-data6
Figure 2 ADCIGs for a synthetic data set. Left: Image for only one azimuth ( | 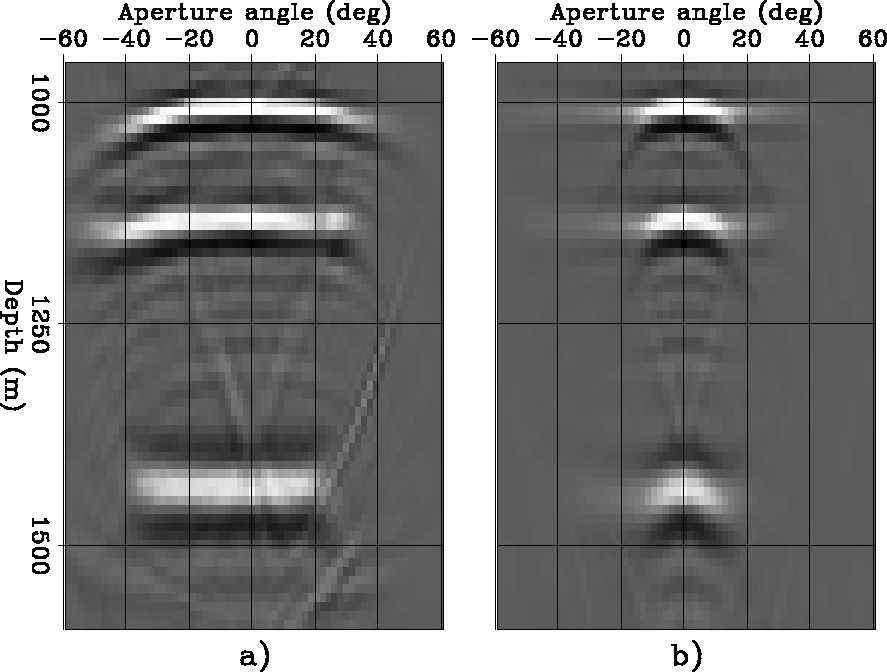 |
The effects of ignoring the
variability in the mapping density
are demonstrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
This figure shows two ADCIGs obtained by imaging
a synthetic data set
with a full source-receiver 3-D prestack migration.
The data set
contains 5 dipping planes,
from zero dip to 60 degrees dip.
The azimuth of the planes is 45 degrees
with respect to the direction of the acquisition.
The velocity was
.
This figure shows two ADCIGs obtained by imaging
a synthetic data set
with a full source-receiver 3-D prestack migration.
The data set
contains 5 dipping planes,
from zero dip to 60 degrees dip.
The azimuth of the planes is 45 degrees
with respect to the direction of the acquisition.
The velocity was ![]() km/s,
which corresponds to the upper limit among
the typical gradients found in the Gulf of Mexico.
The acquisition geometry had one single azimuth
and the source-receiver offset range was -1.6-3 km.
More detailed description of this data set can be found in
Biondi (2001, 2003); Vaillant and Biondi (2000).
km/s,
which corresponds to the upper limit among
the typical gradients found in the Gulf of Mexico.
The acquisition geometry had one single azimuth
and the source-receiver offset range was -1.6-3 km.
More detailed description of this data set can be found in
Biondi (2001, 2003); Vaillant and Biondi (2000).
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows an ADCIG
computed at fixed reflection azimuth
a shows an ADCIG
computed at fixed reflection azimuth ![]() of 16 degrees.
This azimuth corresponds
- only approximately, because the reflection azimuth changes with the
aperture angle -
to the reflection azimuth for the deepest reflector.
Correspondingly, the deepest reflector
has a flat moveout along the aperture angles,
but the shallower ones are frowning downward.
Figure
of 16 degrees.
This azimuth corresponds
- only approximately, because the reflection azimuth changes with the
aperture angle -
to the reflection azimuth for the deepest reflector.
Correspondingly, the deepest reflector
has a flat moveout along the aperture angles,
but the shallower ones are frowning downward.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b shows the result of averaging
over azimuths all the ADCIGS within the
range of
b shows the result of averaging
over azimuths all the ADCIGS within the
range of ![]() .In this case the moveouts are flat
for all the reflection angles larger than 10 degrees,
but the amplitude
of the image is strongly attenuated for all these angles.
This distortion of the image amplitudes is caused
by the variable density of the mapping from the
the
.In this case the moveouts are flat
for all the reflection angles larger than 10 degrees,
but the amplitude
of the image is strongly attenuated for all these angles.
This distortion of the image amplitudes is caused
by the variable density of the mapping from the
the ![]() plane into the
plane into the
![]() plane
illustrated in Figure
plane
illustrated in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
The solution to this problem seems straightforward.
We can correct the amplitudes by applying
the jacobian of the transformation
from the ![]() plane into the
plane into the
![]() plane
(Appendix A presents the formulas to evaluate the jacobian).
However, while this correction yields a much improved result,
it is not sufficient.
Figure
plane
(Appendix A presents the formulas to evaluate the jacobian).
However, while this correction yields a much improved result,
it is not sufficient.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a shows the effect of including
the jacobian while transforming the image into angle domain.
The amplitudes of the ADCIG are now distorted in the opposite direction
of the previous result
(Figure
a shows the effect of including
the jacobian while transforming the image into angle domain.
The amplitudes of the ADCIG are now distorted in the opposite direction
of the previous result
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b).
Now the wide aperture angles have a good amplitude
response, but the narrow angles have been
too strongly attenuated and
the
b).
Now the wide aperture angles have a good amplitude
response, but the narrow angles have been
too strongly attenuated and
the ![]() trace has been zeroed.
This behavior is simply explained by the fact
that the jacobian is zero at
trace has been zeroed.
This behavior is simply explained by the fact
that the jacobian is zero at ![]() .This singularity of the jacobian
is graphically represented in
Figure
.This singularity of the jacobian
is graphically represented in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) by the
fact that all the dots corresponding
to
by the
fact that all the dots corresponding
to ![]() fall into the origin
of the plane, where the
dot density becomes effectively infinite.
fall into the origin
of the plane, where the
dot density becomes effectively infinite.
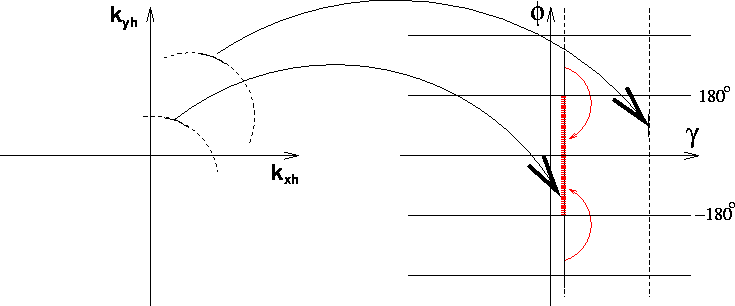
A simple solution to this problem is suggested
when we examine the inverse mapping,
as it is graphically illustrated in the
sketch in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
In this case an integration segment along the line
defined by constant
.
In this case an integration segment along the line
defined by constant ![]() and close
to the origin of
the
and close
to the origin of
the ![]() plane would expand
into a long segment extending
well beyond
the usual range of
plane would expand
into a long segment extending
well beyond
the usual range of ![]() .However, because of the periodicity of the mapping,
the segment is actually folded into the
the
.However, because of the periodicity of the mapping,
the segment is actually folded into the
the ![]() ,and its effective length is limited to 360 degrees (
,and its effective length is limited to 360 degrees (![]() ).
Taking into account of this fact,
we can correct the jacobian weighting
and recover the image amplitudes close to normal incidence.
The details of the correction and its derivation are presented
in Appendix A.
).
Taking into account of this fact,
we can correct the jacobian weighting
and recover the image amplitudes close to normal incidence.
The details of the correction and its derivation are presented
in Appendix A.
The effects of taking into account the folding of the
azimuth axis in the mapping are demonstrated in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b.
Now the angles close to near incidence have
been properly imaged.
Figure
b.
Now the angles close to near incidence have
been properly imaged.
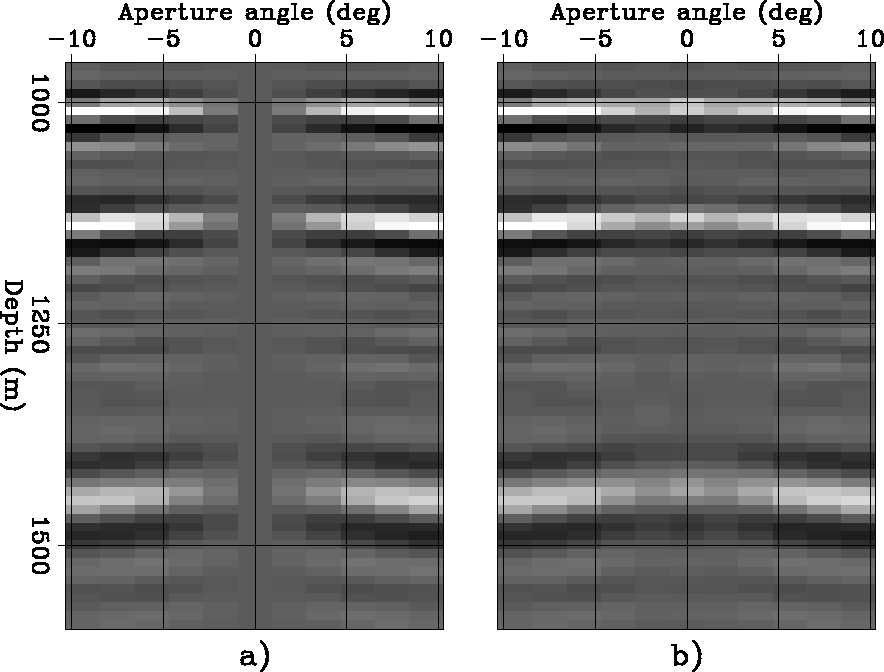
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows windows of the ADCIGs
shown in Figure
shows windows of the ADCIGs
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with narrower aperture angle ranges.
The comparison of
Figure
with narrower aperture angle ranges.
The comparison of
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) a
and
Figure
a
and
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) b
demonstrates the improvements achieved
by taking into account the folding of the
azimuth axis.
b
demonstrates the improvements achieved
by taking into account the folding of the
azimuth axis.
|
cig-2-data6
Figure 3 ADCIGs for a synthetic data set. Left: Image obtained when the simple jacobian weighting is applied before averaging over azimuths. Right: Image obtained when the jacobian weighting takes into account the folding of the azimuth axis. |  |
 |
|
cig-2-data6-win
Figure 5 Zoom into the ADCIGS shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) to examine the differences between the two panels
close to normal incidence.
to examine the differences between the two panels
close to normal incidence.
|  |
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrate the effect of the amplitude correction from another point of view.
They show depth slices taken at the depth of 1,140 meters
(corresponding to the reflector dipping at 45 degrees)
before the stacking over azimuths.
The reflection amplitudes are thus shown as function of
both the aperture angle
illustrate the effect of the amplitude correction from another point of view.
They show depth slices taken at the depth of 1,140 meters
(corresponding to the reflector dipping at 45 degrees)
before the stacking over azimuths.
The reflection amplitudes are thus shown as function of
both the aperture angle ![]() and the azimuth
and the azimuth ![]() .Because of the poor azimuthal resolution close to normal incidence,
the azimuthal range is wide for small
.Because of the poor azimuthal resolution close to normal incidence,
the azimuthal range is wide for small ![]() ;it narrows as
;it narrows as ![]() increases.
Comparing Figure
increases.
Comparing Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with
Figure
with
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) it is evident that the amplitude correction
boost up the relative amplitudes of the image at large
it is evident that the amplitude correction
boost up the relative amplitudes of the image at large
![]() .
.
|
zaz-60-60-dense-all-v3-data6
Figure 6 Depth slice taken at the depth of 1,140 meters (corresponding to the reflector dipping at 45 degrees) before the stacking over azimuths. Notice that the azimuthal resolution is strongly dependent on the aperture angle. | 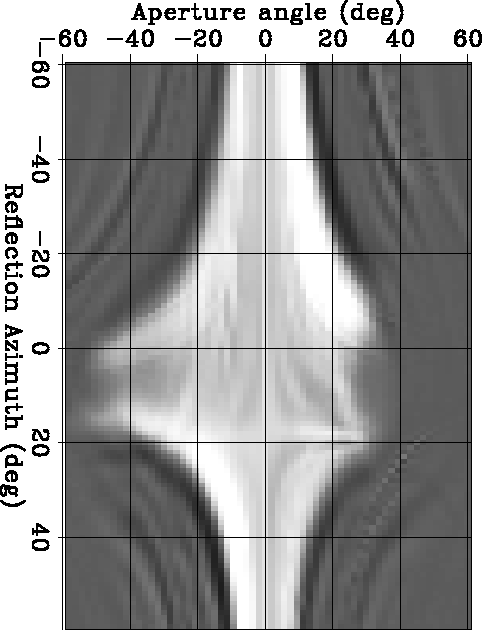 |
|
zaz-60-60-dense-all-jac-v3-data6
Figure 7 Depth slice taken at the same depth as the slice shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) (z=1,1140 meters)
after application of the proposed angular dependent weighting.
Notice that the amplitudes close to normal incidence
have been attenuated, but not zeroed,
and the ones at large aperture angle
have been boosted up.
(z=1,1140 meters)
after application of the proposed angular dependent weighting.
Notice that the amplitudes close to normal incidence
have been attenuated, but not zeroed,
and the ones at large aperture angle
have been boosted up.
|  |