




Next: Conclusions
Up: Regularization Schemes
Previous: Gradient magnitude and Laplacian
Until now we have used a roughener as the regularization operator to take into account the prior knowledge that letters are piecewise constant. Turning it off at the edges and on away from the edges.
To do the opposite also makes sense, using a smoothing operator at the edges and turning it off away from the edges doesn't make the model smoother away from the edges but increases the sharpness of the model at the edges.
The gradient magnitude with triangular smoothing edge-preserving regularization fitting goal was set
following the nonlinear iterations:
starting with 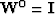 , at the kth iteration the algorithm solves
, at the kth iteration the algorithm solves
| 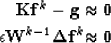 |
|
| (5) |
where
| 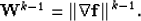 |
(6) |
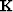 is a non-stationary convolution matrix,
is a non-stationary convolution matrix, 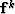 is the result of the kth nonlinear iteration,
is the result of the kth nonlinear iteration, 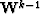 is the (k-1)th diagonal weighting operators,
is the (k-1)th diagonal weighting operators, 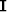 is the identity matrix,
is the identity matrix, 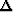 is triangular smoother operator,
and the scalar
is triangular smoother operator,
and the scalar  balances the relative importance of the data and model residuals.
comp_images_smooth_2d
balances the relative importance of the data and model residuals.
comp_images_smooth_2d
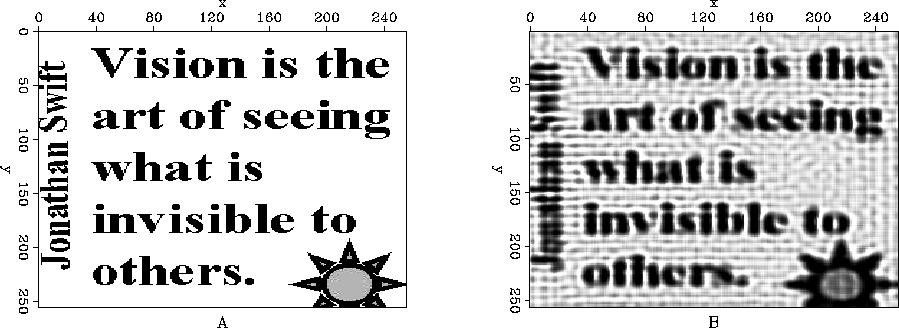
Figure 8 A) Original image, B) Deblurred image using LS with the edge-preserving regularization gradient magnitude with triangular smoothing





comp_graph_2d_smooth
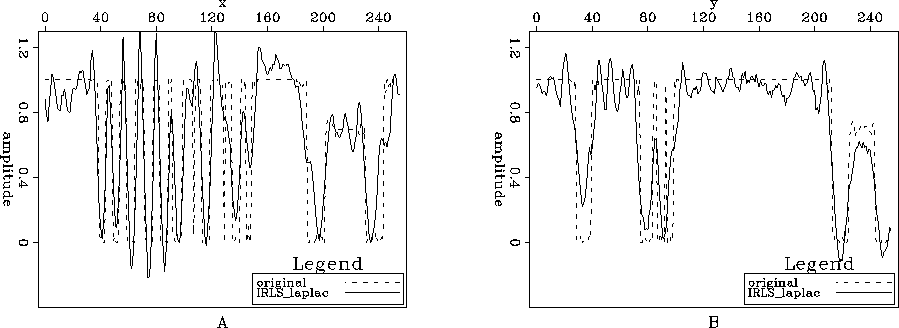
Figure 9 Comparison between Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) A and
A and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) B; A) Slice y=229 and B) Slice x=229of.
B; A) Slice y=229 and B) Slice x=229of.





Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show what we were expecting, i.e. the edges look sharp, but away from the edges the noise dominates. However, we can see in figure
show what we were expecting, i.e. the edges look sharp, but away from the edges the noise dominates. However, we can see in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) some details that we are not visible in Figures
some details that we are not visible in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , and
, and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Looking that a combination of the styling goals in equations (3) (smoothing away from the edges) and (5) (roughening at the edges) should give a good result.
. Looking that a combination of the styling goals in equations (3) (smoothing away from the edges) and (5) (roughening at the edges) should give a good result.





Next: Conclusions
Up: Regularization Schemes
Previous: Gradient magnitude and Laplacian
Stanford Exploration Project
10/14/2003
![]() , at the kth iteration the algorithm solves
, at the kth iteration the algorithm solves
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) A and
A and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) B; A) Slice y=229 and B) Slice x=229of.
B; A) Slice y=229 and B) Slice x=229of.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show what we were expecting, i.e. the edges look sharp, but away from the edges the noise dominates. However, we can see in figure
show what we were expecting, i.e. the edges look sharp, but away from the edges the noise dominates. However, we can see in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) some details that we are not visible in Figures
some details that we are not visible in Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
, ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , and
, and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . Looking that a combination of the styling goals in equations (3) (smoothing away from the edges) and (5) (roughening at the edges) should give a good result.
. Looking that a combination of the styling goals in equations (3) (smoothing away from the edges) and (5) (roughening at the edges) should give a good result.