




Next: Gradient magnitude and smooth
Up: Regularization Schemes
Previous: First order derivative regularization
In the previous section we changed the norm of the minimization problem to prevent the roughener from smoothing over the edges of the model. In this subsection we shift from a statistical to a more mechanical approach to attain the same goal.
The gradient magnitude ( ) is an isotropic edge-detection operator that can be used to calculate the diagonal weights. Unfortunately, it is a nonlinear operator thus couldn't be used for regularization. Instead we used the Laplacian, which is a regularization operator used in several SEP applications Claerbout and Fomel (2001).
) is an isotropic edge-detection operator that can be used to calculate the diagonal weights. Unfortunately, it is a nonlinear operator thus couldn't be used for regularization. Instead we used the Laplacian, which is a regularization operator used in several SEP applications Claerbout and Fomel (2001).
The gradient magnitude edge-preserving regularization fitting goal was set
following the nonlinear iterations:
starting with 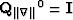 , at the kth iteration the algorithm solves
, at the kth iteration the algorithm solves
| 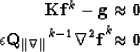 |
|
| (3) |
where
| 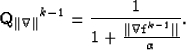 |
(4) |
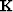 is a non-stationary convolution matrix,
is a non-stationary convolution matrix, 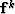 is the result of the kth nonlinear iteration,
is the result of the kth nonlinear iteration, 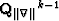 is the (k-1)th diagonal weighting operators,
is the (k-1)th diagonal weighting operators, 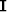 is the identity matrix,
is the identity matrix,  is the gradient magnitude,
is the gradient magnitude, 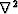 is the Laplacian operator, the scalar
is the Laplacian operator, the scalar  is the trade-off parameter controlling the discontinuities in the solution,
and the scalar
is the trade-off parameter controlling the discontinuities in the solution,
and the scalar  balances the relative importance of the data and model residuals.
balances the relative importance of the data and model residuals.
comp_images_laplac_2d
Figure 6 A) Original image, B) Deblurred image using LS with the gradient magnitude edge-preserving regularization ( ) with laplacian edge-preserving regularization
) with laplacian edge-preserving regularization





comp_graph_2d_laplac
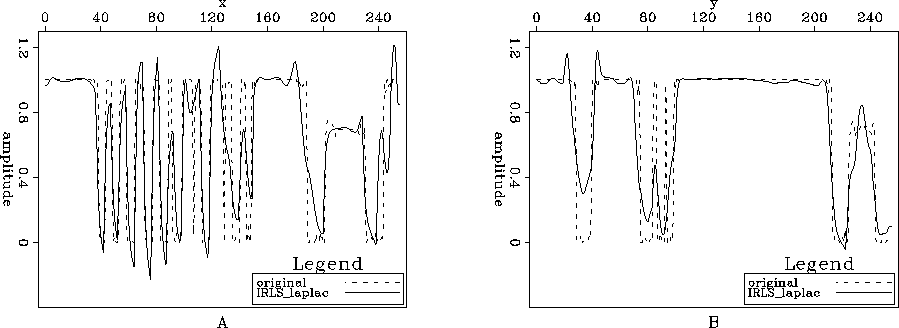
Figure 7 Comparison between Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) A and
A and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) B; A) Slice y=229 and B) Slice x=229.
B; A) Slice y=229 and B) Slice x=229.





Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show a considerable improvement over Figures
show a considerable improvement over Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . They are noise free but keep the round features of the original image. However, since we are not imposing blockiness on the model but rather on the derivative of the model (using the Laplacian as the regularization operator), the edges are not as sharp as the previous case.
. They are noise free but keep the round features of the original image. However, since we are not imposing blockiness on the model but rather on the derivative of the model (using the Laplacian as the regularization operator), the edges are not as sharp as the previous case.





Next: Gradient magnitude and smooth
Up: Regularization Schemes
Previous: First order derivative regularization
Stanford Exploration Project
10/14/2003
![]() ) is an isotropic edge-detection operator that can be used to calculate the diagonal weights. Unfortunately, it is a nonlinear operator thus couldn't be used for regularization. Instead we used the Laplacian, which is a regularization operator used in several SEP applications Claerbout and Fomel (2001).
) is an isotropic edge-detection operator that can be used to calculate the diagonal weights. Unfortunately, it is a nonlinear operator thus couldn't be used for regularization. Instead we used the Laplacian, which is a regularization operator used in several SEP applications Claerbout and Fomel (2001).
![]() , at the kth iteration the algorithm solves
, at the kth iteration the algorithm solves
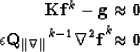
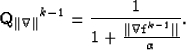

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) A and
A and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) B; A) Slice y=229 and B) Slice x=229.
B; A) Slice y=229 and B) Slice x=229.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) show a considerable improvement over Figures
show a considerable improvement over Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . They are noise free but keep the round features of the original image. However, since we are not imposing blockiness on the model but rather on the derivative of the model (using the Laplacian as the regularization operator), the edges are not as sharp as the previous case.
. They are noise free but keep the round features of the original image. However, since we are not imposing blockiness on the model but rather on the derivative of the model (using the Laplacian as the regularization operator), the edges are not as sharp as the previous case.