




Next: Gradient magnitude and Laplacian
Up: Regularization Schemes
Previous: Regularization Schemes
A way of forcing a function to be piecewise constant is forcing its first order derivatives to be sparse.
Thus, using a first order derivative regularization operator and forcing the model residuals to follow a Cauchy distribution should make the letters ``blocky'' and preserve the letter edges Youzwishen (2001). Obtaining model residuals following a Cauchy distribution can be achieve posing the inverse problem as Iterative Reweighed Least Squares (IRLS) Darche (1989).
The Cauchy norm first order derivative edge-preserving regularization fitting goal was set
following the nonlinear iterations:
starting with  , at the kth iteration the algorithm solves
, at the kth iteration the algorithm solves
| 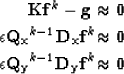 |
|
| |
| (1) |
where
| ![\begin{eqnarray}
{\bf Q_{x}}^{k-1} = \frac{1}{\left[1+\left( \frac{{ \bf D_x f}^...
...frac{{ \bf D_y f}^{k-1}}{\alpha} \right)^2 \right]^{\frac{1}{2}}}.\end{eqnarray}](img6.gif) |
|
| (2) |
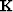 is a non-stationary convolution matrix,
is a non-stationary convolution matrix, 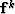 is the result of the kth nonlinear iteration,
is the result of the kth nonlinear iteration, 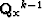 and
and 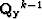 are the (k-1)th diagonal weighting operators, and
are the (k-1)th diagonal weighting operators, and 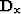 and
and 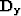 are the first order derivative operator in the x and y directions,
are the first order derivative operator in the x and y directions, 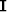 is the identity matrix, the scalar
is the identity matrix, the scalar  is the trade-off parameter controlling the discontinuities in the solution, and the scalar
is the trade-off parameter controlling the discontinuities in the solution, and the scalar  balances the relative importance of the data and model residuals.
balances the relative importance of the data and model residuals.
comp_images_2d
Figure 4 A) Original image, B) Deblurred image using LS with the first order derivative edge-preserving regularization





comp_graph_2d
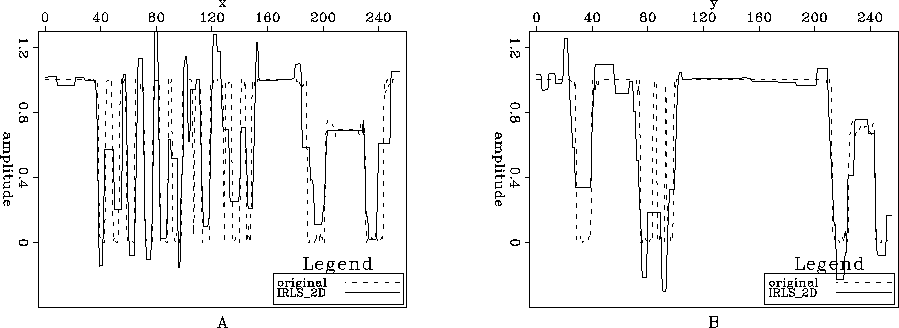
Figure 5 Comparison between Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) A and
A and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) B; A) Slice y=229 and B) Slice x=229.
B; A) Slice y=229 and B) Slice x=229.





We were successful in obtaining what we designed the algorithm to produce. The result is blocky in the x and y directions (Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). However, the derivatives in the x and y directions do not produce an isotropic result. We know that letters often have round shapes. Thus, the problem could benefit from using a more isotropic operator to calculate the diagonal weights.
). However, the derivatives in the x and y directions do not produce an isotropic result. We know that letters often have round shapes. Thus, the problem could benefit from using a more isotropic operator to calculate the diagonal weights.





Next: Gradient magnitude and Laplacian
Up: Regularization Schemes
Previous: Regularization Schemes
Stanford Exploration Project
10/14/2003
![]() , at the kth iteration the algorithm solves
, at the kth iteration the algorithm solves
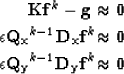
![\begin{eqnarray}
{\bf Q_{x}}^{k-1} = \frac{1}{\left[1+\left( \frac{{ \bf D_x f}^...
...frac{{ \bf D_y f}^{k-1}}{\alpha} \right)^2 \right]^{\frac{1}{2}}}.\end{eqnarray}](img6.gif)

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) A and
A and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) B; A) Slice y=229 and B) Slice x=229.
B; A) Slice y=229 and B) Slice x=229.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). However, the derivatives in the x and y directions do not produce an isotropic result. We know that letters often have round shapes. Thus, the problem could benefit from using a more isotropic operator to calculate the diagonal weights.
). However, the derivatives in the x and y directions do not produce an isotropic result. We know that letters often have round shapes. Thus, the problem could benefit from using a more isotropic operator to calculate the diagonal weights.