




Next: L norm to handle
Up: VARIABLE EPSILON
Previous: VARIABLE EPSILON
Following the methodology of Clapp and Biondi (1999), I will
begin by considering a regularized tomography problem.
I will linearize around an initial slowness estimate and find
a linear operator in the vertical
traveltime domain 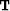 between our change in slowness
between our change in slowness 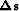 and our change in traveltimes
and our change in traveltimes 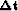 .We will write a set of fitting goals,
.We will write a set of fitting goals,
| 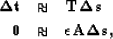 |
|
| (1) |
where 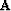 is our steering filter operator Clapp et al. (1997) and
is our steering filter operator Clapp et al. (1997) and  is a
Lagrange multiplier.
However, these
fitting goals don't accurately describe what
we really want. Our steering filters are based on our
desired slowness rather than change of slowness. With this
fact in mind, we can rewrite our second fitting goal as:
is a
Lagrange multiplier.
However, these
fitting goals don't accurately describe what
we really want. Our steering filters are based on our
desired slowness rather than change of slowness. With this
fact in mind, we can rewrite our second fitting goal as:
| 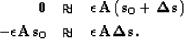 |
(2) |
| |
Our second fitting goal can not be strictly defined as regularization
but we can still do a preconditioning substitution Fomel et al. (1997),
giving us a new set of fitting goals:
| 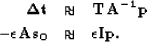 |
|
| (3) |
Our standard inversion fitting goals (3) make an assumption that
our data fitting goal is equally believable everywhere. Stated another way,
we want the same weight  for our model styling goal everywhere.
This is generally untrue. We can, and should, account for differing
level of confidence in two different ways.
If we have a measure of certainty about a data point (for example how much
of a peak our semblance pick is) we can add a data covariance operator
for our model styling goal everywhere.
This is generally untrue. We can, and should, account for differing
level of confidence in two different ways.
If we have a measure of certainty about a data point (for example how much
of a peak our semblance pick is) we can add a data covariance operator 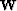 to
our fitting goals,
to
our fitting goals,
| 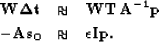 |
|
| (4) |
We can also often make statements about our confidence in our data fitting goal
as a function of our model space. For example, generally as we get deeper, we
will have less confidence in the points, and be less able to get a high frequency
velocity model. We can account for this uncertainty by
replacing the constant epsilon of fitting goal (4)
with a diagonal weighting operator 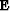 resulting in the updated fitting goals,
resulting in the updated fitting goals,
| 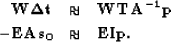 |
|
| (5) |
By having this additional freedom we can allow for more model
variability in the near surface and force more smoothing
at deeper locations.
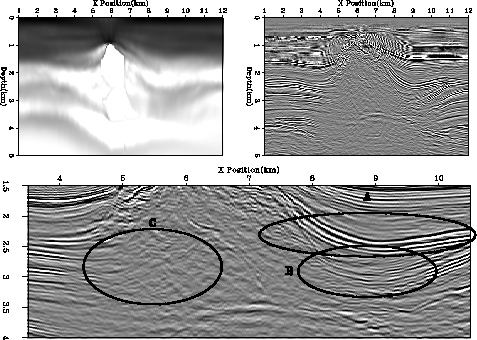
Figure 6 shows the result of using the
new fitting goals (5). Note how we have
a higher frequency velocity structure above and a smoother
below. The overall image quality is also improved compared
to Figure 5.
combo.vel1.eps
Figure 6 Data after one iteration using a constant  .
The top-left panel shows the velocity
model and the top-right panel shows the migrated
image using this velocity.
The bottom panel shows a zoomed area around the salt body.
Note the salt
bottom,`A'; the valley structure at `B'; and under the salt over-hang at `C'.
Note the improved image quality compared to Figure 4 and
Figure 5.
.
The top-left panel shows the velocity
model and the top-right panel shows the migrated
image using this velocity.
The bottom panel shows a zoomed area around the salt body.
Note the salt
bottom,`A'; the valley structure at `B'; and under the salt over-hang at `C'.
Note the improved image quality compared to Figure 4 and
Figure 5.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: L norm to handle
Up: VARIABLE EPSILON
Previous: VARIABLE EPSILON
Stanford Exploration Project
11/11/2002
![]() resulting in the updated fitting goals,
resulting in the updated fitting goals,
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)