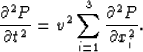Next: New notations and definitions
Up: Appendix
Previous: Appendix
Let xi, where i=1,2,3 be three orthogonal directions and 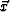 the position vector in a coordinate system associated with the three
directions. Let us define
the position vector in a coordinate system associated with the three
directions. Let us define 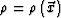 as
the mass per volume unit in the acoustic medium,
as
the mass per volume unit in the acoustic medium, 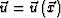 as the velocity of the acoustic medium and K
as the bulk modulus of the acoustic medium. The second law of dynamics
states that mass
as the velocity of the acoustic medium and K
as the bulk modulus of the acoustic medium. The second law of dynamics
states that mass 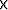 acceleration = force = - pressure gradient:
acceleration = force = - pressure gradient:
| 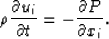 |
(15) |
Energy can be stored by compression and volume variation. If
| 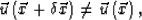 |
(16) |
we say that the flow diverges (the volume changes). This leads to a
pressure variation, proportional to the divergence of the velocity:
| 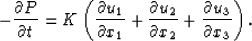 |
(17) |
The wave equation in an acoustic medium can be deduced from
(15) and (17) as follows. Derivate (17)
with respect to time:
| 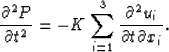 |
(18) |
Divide (15) by 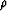 and derivate it with respect to the
axis xi:
and derivate it with respect to the
axis xi:
| 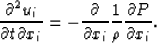 |
(19) |
Plug (19) in (18):
| 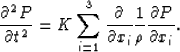 |
(20) |
Approximation: 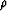 is a constant that does not depend on the
position vector. By denoting the acoustic waves propagation velocity
through the medium by v, where
is a constant that does not depend on the
position vector. By denoting the acoustic waves propagation velocity
through the medium by v, where
| 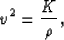 |
(21) |
we obtain the acoustic wave equation:
| 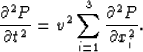 |
(22) |





Next: New notations and definitions
Up: Appendix
Previous: Appendix
Stanford Exploration Project
6/8/2002
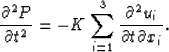
![]() and derivate it with respect to the
axis xi:
and derivate it with respect to the
axis xi:
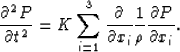
![]() is a constant that does not depend on the
position vector. By denoting the acoustic waves propagation velocity
through the medium by v, where
is a constant that does not depend on the
position vector. By denoting the acoustic waves propagation velocity
through the medium by v, where