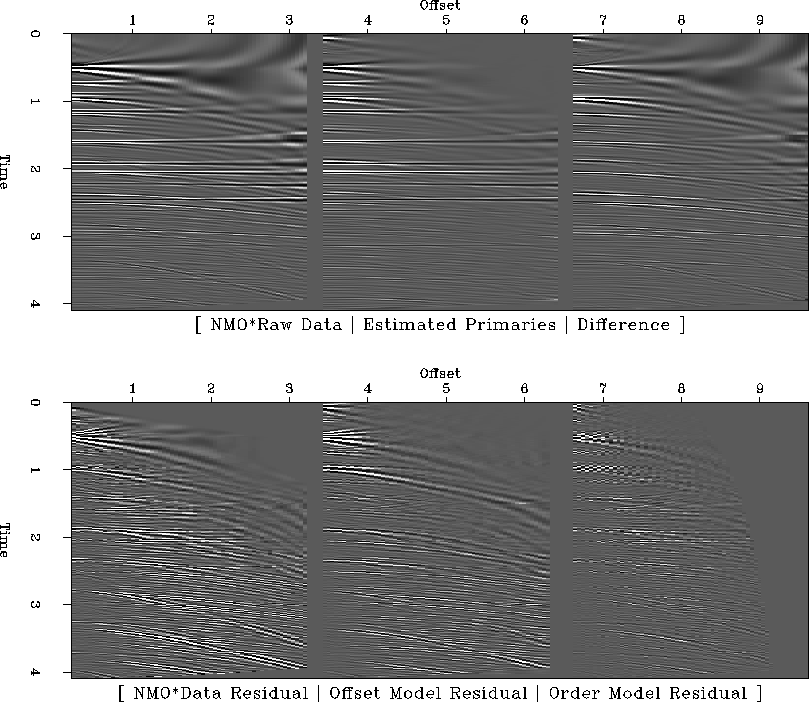
Figure 4 illustrates the application of the proposed algorithm to the
so-called ``Haskell'' data. Comparing the raw data and the estimated primary panels
[![]() in equation (6)], we see that my algorithm does a decent job of
suppressing the strongest multiples, especially at far offsets, though some residual multiple
energy remains at the near offsets. We expect poorer performance at near offsets; recall that
the first regularization operator [equation (8)] penalizes dissimilarity of
events across orders of multiple, yet all orders of multiple align at near offsets. Moreover,
the second regularization operator [equation (9)] penalizes residual curvature,
yet all events in the section, both primaries and the residual multiples, are flat at near offsets.
in equation (6)], we see that my algorithm does a decent job of
suppressing the strongest multiples, especially at far offsets, though some residual multiple
energy remains at the near offsets. We expect poorer performance at near offsets; recall that
the first regularization operator [equation (8)] penalizes dissimilarity of
events across orders of multiple, yet all orders of multiple align at near offsets. Moreover,
the second regularization operator [equation (9)] penalizes residual curvature,
yet all events in the section, both primaries and the residual multiples, are flat at near offsets.
The difference panel shows little residual primary energy, which illustrates the favorable signal preservation capability of my approach. The bulk of the residual primary energy exists at far offsets and small times, where NMO stretch makes the primaries nonflat, and hence, vulnerable to smoothing across offset by equation (9).
The bottom three panels in Figure 4 show the data residual [equation (7)], and the first two panels of the two model residuals [equations (9) and (8), respectively]. Put simply, the data residual consists of events which are not modeled by equation (6) - hopefully, the multiples only. The model residuals consist roughly of the portions of the model which were removed by the two regularization terms (again, hopefully multiples only): high-wavenumber events and events which are inconsistent from one panel to the next.
 |