Least-squares imaging of multiples

Applied to a common-midpoint gather, equation (1) produces an approximate unstacked zero-offset image of pseudo-primaries from water bottom multiple reflections. In this section, I introduce a least squares scheme to compute self-consistent images of primaries and pseudo-primaries which are in turn consistent with the data. First I define some terms: With these definitions in hand, we can now write the forward modeling operator for joint NMO of primaries and multiples of order 1 to p.  

$$\left[ \bold N_0 \ \ \bold N_1 \bold R_1 \ \cdots \ \bold N_... ...old m_1 \\ \vdots \\ \bold m_p \end{array} \right] = \bf Lm$$ (6)

In words, equation (6) takes a collection of psuedo-primary panels, divides each by the appropriate reflection coefficient, applies inverse (adjoint) NMO to each, and then sums them together to create something that should resemble ``data''. We define the data residual as the difference between the input data and the forward-modeled data:  

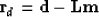$$\bold r_d = \bf d - Lm$$ (7)

Viewed as a standard least-squares inversion problem, minimization of L₂ norm of the data residual by solution of the normal equations is underdetermined. Additional regularization terms, defined in later sections, force the problem to be overdetermined.