




Next: Estimation of systematic error
Up: Brown: Systematic error estimation
Previous: Introduction
The simplest inverse interpolation approach outlined in Claerbout (1999) can be written
in least squares fitting goals as follows.
| 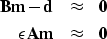 |
|
| (1) |
boldB is nearest neighbor interpolation and maps a gridded model (m) to the
irregular data space (d). The model grid is 860x500 points, while the data space
consists of over 132,000 (x,y,z) triples. A is a model regularization operator,
which penalizes model roughness. For all examples contained herein, 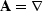 .
.
 balances the tradeoff between data fitting and spatial model smoothness.
balances the tradeoff between data fitting and spatial model smoothness.
To handle non-gaussian noise, Fomel and Claerbout (1995) implement an Iteratively Reweighted
Least Squares (IRLS) scheme to nonlinearly estimate a residual weight which automatically reduces
the importance of ``bad'' data in least squares estimation. Adding a diagonal residual weight to
equation (1) gives
| 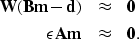 |
|
| (2) |
To handle systematic errors between data tracks, Fomel and Claerbout (1995) supplement
the residual weight in system (1) with a first derivative filter to decorrelate
the residual. Lomask (1998) used a single prediction error filter (PEF).
Karpushin and Brown (2001) use a bank of PEF's, one for each acquisition track.
Whatever the case, we can refer to the differential operator as D and modify equation
(2) to obtain a new system of equations:
| 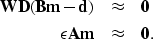 |
|
| (3) |
W is the same as in equation (2), except for the addition of
zero weights at track boundaries.





Next: Estimation of systematic error
Up: Brown: Systematic error estimation
Previous: Introduction
Stanford Exploration Project
9/18/2001