




Next: Normalization of Kirchhoff operators
Up: Normalization by operator fold
Previous: Introduction
Operator fold is defined as the impulse response of the
operator to an input vector full of ones.
To understand this concept more clearly, it is
best to begin with a very simple operator: nearest neighbour
interpolation (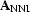 ) and its adjoint (binning).
For this operator, the Hessian matrix,
) and its adjoint (binning).
For this operator, the Hessian matrix,
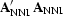 , is
exactly diagonal, and it would be possible to calculate the diagonal
values accurately with any reasonable choice of reference model in
equation (
, is
exactly diagonal, and it would be possible to calculate the diagonal
values accurately with any reasonable choice of reference model in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). A particularly simple choice of
reference model is to fill the model-space with ones. Since the
operator is nearest-neighbour interpolation, this results in a
data-space full of ones too.
Binning this data vector gives the fold of the operator in model-space
Claerbout (1998a); and its inverse can be used directly as a weighting
function for inverse nearest neighbour interpolation,
). A particularly simple choice of
reference model is to fill the model-space with ones. Since the
operator is nearest-neighbour interpolation, this results in a
data-space full of ones too.
Binning this data vector gives the fold of the operator in model-space
Claerbout (1998a); and its inverse can be used directly as a weighting
function for inverse nearest neighbour interpolation,
| 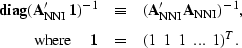 |
(130) |
| |
For an example that is slightly more complex than nearest neighbour
interpolation, consider linear interpolation.
The Hessian matrix for linear
interpolation, 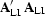 is
tridiagonal rather than exactly diagonal; therefore, unless we know
the true solution, any diagonal operator that we produce will be an
approximation. This leads to a conundrum: is it better to find the
diagonal of
is
tridiagonal rather than exactly diagonal; therefore, unless we know
the true solution, any diagonal operator that we produce will be an
approximation. This leads to a conundrum: is it better to find the
diagonal of 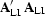 , or another
approximation that incorporates information about the off-diagonal
elements?
, or another
approximation that incorporates information about the off-diagonal
elements?
Following the same approach as above, a vector full of ones seems a
reasonable choice for a reference model; and as before, this generates
a data vector full of ones.
Applying the adjoint of linear interpolation to this data
vector produces the model-space fold, 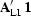 ,that can be used in the approximation,
,that can be used in the approximation,
| 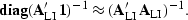 |
(131) |
The fold of the linear interpolation operator is not the diagonal of
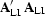 , but rather the sum along the
rows of
, but rather the sum along the
rows of 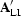 Chemingui (1999), which for the case of
any interpolator is equivalent to the row-sums of
Chemingui (1999), which for the case of
any interpolator is equivalent to the row-sums of
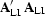 Biondi (1997).
The distinction between taking the diagonal and the row-based sum is
an important one because equation (
Biondi (1997).
The distinction between taking the diagonal and the row-based sum is
an important one because equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is exact if the
true model is a constant function, and will be a good approximation if
the true model is smooth compared to the size of
an impulse response of
) is exact if the
true model is a constant function, and will be a good approximation if
the true model is smooth compared to the size of
an impulse response of 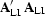 (two
sample intervals).
As long as this smoothness requirement is satisfied,
equation (
(two
sample intervals).
As long as this smoothness requirement is satisfied,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) implies that a row-based
normalization function is better than the diagonal itself.
) implies that a row-based
normalization function is better than the diagonal itself.
Figures ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) strengthens this
conclusion.
The top panels show a simple regularly-sampled model consisting of a
four events. The middle panels show data-points obtained by
linear interpolation from this model, and the lower panels show the
reestimated models after normalized binning with the adjoint of the
linear interpolator. The thin solid-lines, the dashed-lines and the
dotted-lines show the true model and the results of normalization by
the matrix diagonal and operator fold, respectively.
strengthens this
conclusion.
The top panels show a simple regularly-sampled model consisting of a
four events. The middle panels show data-points obtained by
linear interpolation from this model, and the lower panels show the
reestimated models after normalized binning with the adjoint of the
linear interpolator. The thin solid-lines, the dashed-lines and the
dotted-lines show the true model and the results of normalization by
the matrix diagonal and operator fold, respectively.
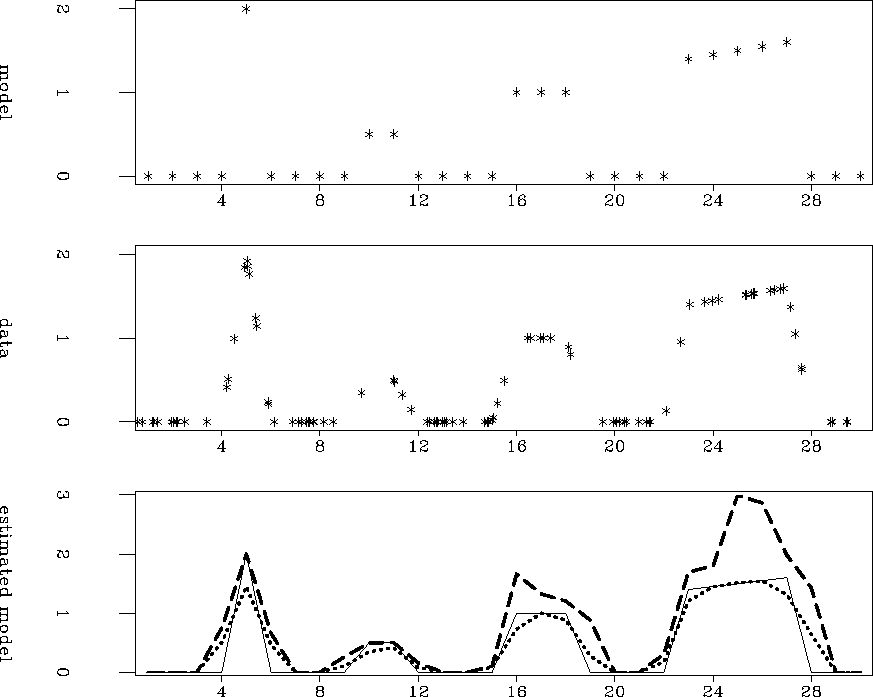
For Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I sampled one hundred data points.
Only where the model consists of an isolated single spike (at
m5) does the diagonal normalization out-perform operator
fold. Elsewhere the amplitude of the original function is recovered
more accurately by operator fold.
For Figure
, I sampled one hundred data points.
Only where the model consists of an isolated single spike (at
m5) does the diagonal normalization out-perform operator
fold. Elsewhere the amplitude of the original function is recovered
more accurately by operator fold.
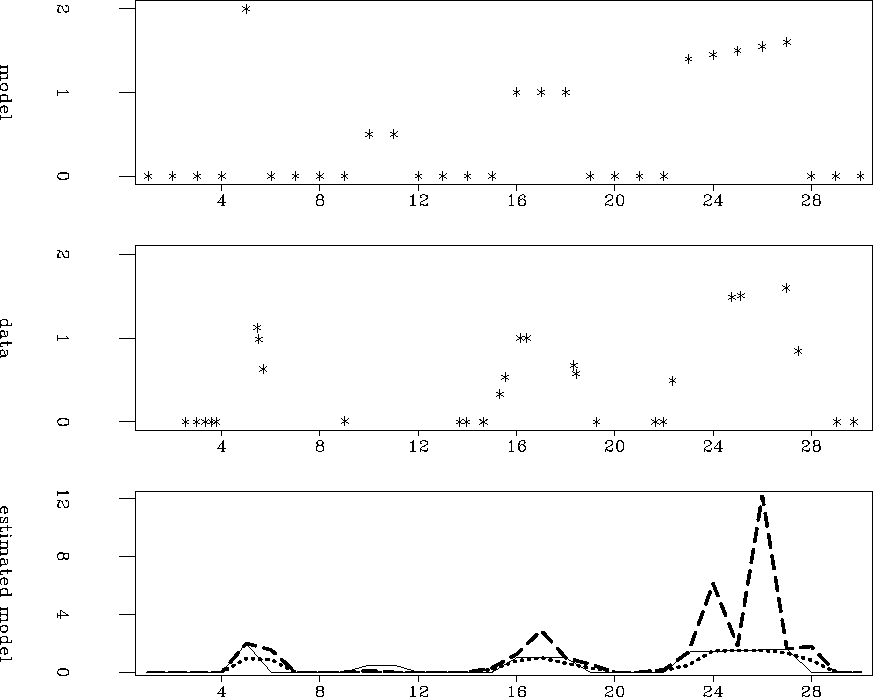
For Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) , I only sampled 30 data points,
leading to a less well-conditioned system than
Figure
, I only sampled 30 data points,
leading to a less well-conditioned system than
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The row-based fold normalization scheme shows itself to be more robust
in areas of poor coverage than the scheme that considers only the
diagonal elements of the
.
The row-based fold normalization scheme shows itself to be more robust
in areas of poor coverage than the scheme that considers only the
diagonal elements of the 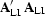 matrix.
matrix.
linterp100
Figure 1 Comparison of normalizing adjoint
linear interpolation with the row-sum of 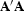 as opposed
to its diagonal. Top panel shows the model. Center panel shows
100 interpolated data points. Lower panel shows reestimated data:
dashed-line after diagonal normalization, dotted-line after
column-based normalization. The solid-line shows the true model. as opposed
to its diagonal. Top panel shows the model. Center panel shows
100 interpolated data points. Lower panel shows reestimated data:
dashed-line after diagonal normalization, dotted-line after
column-based normalization. The solid-line shows the true model.
|
|  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





linterp30
Figure 2 Same as Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ,
but with only 30 data points. The diagonal-based approach
(dashed-line) is less robust in areas of poor coverage than the
row-sum approach (dotted-line). ,
but with only 30 data points. The diagonal-based approach
(dashed-line) is less robust in areas of poor coverage than the
row-sum approach (dotted-line).
|
|  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: Normalization of Kirchhoff operators
Up: Normalization by operator fold
Previous: Introduction
Stanford Exploration Project
5/27/2001
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). A particularly simple choice of
reference model is to fill the model-space with ones. Since the
operator is nearest-neighbour interpolation, this results in a
data-space full of ones too.
Binning this data vector gives the fold of the operator in model-space
Claerbout (1998a); and its inverse can be used directly as a weighting
function for inverse nearest neighbour interpolation,
). A particularly simple choice of
reference model is to fill the model-space with ones. Since the
operator is nearest-neighbour interpolation, this results in a
data-space full of ones too.
Binning this data vector gives the fold of the operator in model-space
Claerbout (1998a); and its inverse can be used directly as a weighting
function for inverse nearest neighbour interpolation,

![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
