Non-stationary factorization

In order to extrapolate waves, we must invert a non-stationary filtering operator. But before we can perform recursive inverse filtering with equation (), we must factor the filter into causal and anticausal components.

Figure  illustrates a process for factorizing a non-stationary filtering matrix. This approach is accurate if the filters vary smoothly in space, and it is the approach that I follow for the examples in this chapter.

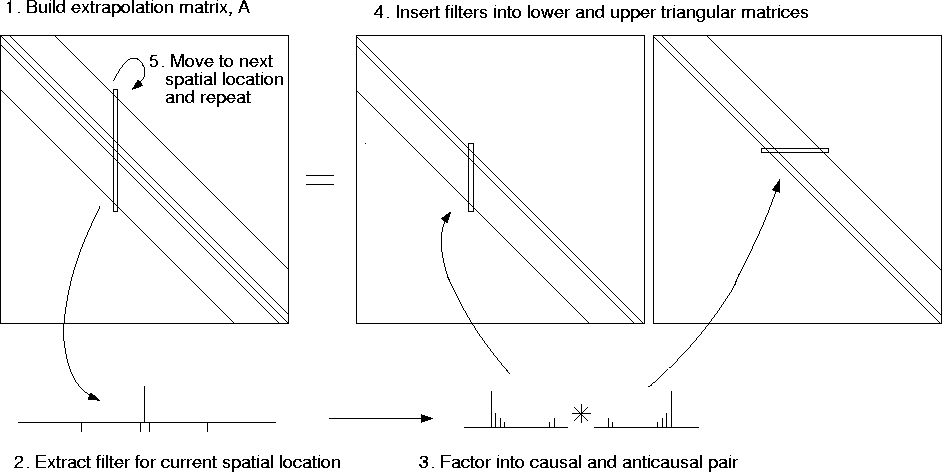
The first step is to build the extrapolation matrix. Then we can extract the impulse response associated with each spatial location, and factor it into causal and anticausal components. By inserting the causal components into the column of a lower triangular matrix, and the anticausal components into a row of an upper triangular matrix, we can begin to build the two invertible matrices. The process has to be repeated for each spatial location.

 

nsfactor
Figure 1 Schematic illustrating non-stationary factorization process. Step 1: Build the extrapolation matrix. Step 2: Extract the filter corresponding to the current spatial location. Step 3: Factor this filter. Step 4: Insert factors into lower and upper triangular matrices. Step 5: Move to next spatial location and repeat from step 2.

In practice, we can save time by factoring the filters in advance, and storing them in a table. For every value of $\omega / v$, we precompute the factors of the 1-D helical filter, $a(\omega /v)$, and store filter coefficients in a look-up table. We then extrapolate the wavefield by non-stationary convolution [equation ()], followed by non-stationary polynomial division with equation ().

Since we interpolate filters, not downward continued wavefields as in phase-shift plus interpolation migration Gazdag and Sguazzero (1984), the number of reference velocities used has minimal effect on the overall cost of the migration. Indeed, the cost of this process is proportional to the number of grid nodes times the number of filter coefficients; so for a fixed number of filter coefficients, the cost is linear in the number of grid nodes [O(N)].