




Next: Non-stationary factorization
Up: Smooth lateral variations in
Previous: Smooth lateral variations in
If the velocity varies smoothly in space, then we can extend the
stationary theory to cover spatially-variable filtering.
Rather than filtering with the stationary forward and inverse
convolution equations,
| 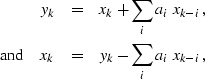 |
(46) |
| (47) |
we can extend the concept of a filter to that of a filter-bank with
one filter for every location in the input/output space
Claerbout (1998a); Margrave (1998).
Now equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
become
)
become
| 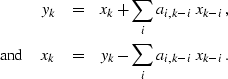 |
(48) |
| (49) |
Non-stationary convolution and recursive inverse convolution are
indeed true inverse processes, but like stationary polynomial
condition non-stationary inverse filtering has potential stability
problems.
Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) discusses this in more detail; it also
demonstrates that, in general, the stability of recursive
non-stationary inverse filtering is not guaranteed even if the
individual filters that make up the filter-bank are all minimum
phase.
discusses this in more detail; it also
demonstrates that, in general, the stability of recursive
non-stationary inverse filtering is not guaranteed even if the
individual filters that make up the filter-bank are all minimum
phase.





Next: Non-stationary factorization
Up: Smooth lateral variations in
Previous: Smooth lateral variations in
Stanford Exploration Project
5/27/2001
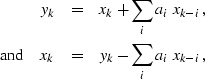
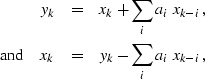
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
become
)
become
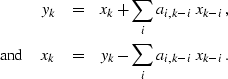
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) discusses this in more detail; it also
demonstrates that, in general, the stability of recursive
non-stationary inverse filtering is not guaranteed even if the
individual filters that make up the filter-bank are all minimum
phase.
discusses this in more detail; it also
demonstrates that, in general, the stability of recursive
non-stationary inverse filtering is not guaranteed even if the
individual filters that make up the filter-bank are all minimum
phase.