![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the results of the new extrapolation
procedure with the conventional Crank-Nicolson solution to the
45
compares the results of the new extrapolation
procedure with the conventional Crank-Nicolson solution to the
45
Fourier transform input data over time-axis
Loop over frequency {
Initialize wave at z=0
Factor wave equation for this w/v
Recursively divide input data by factor
Fourier Transform back to time-domain
Sum into output
}
Incorporating this code into the Wavemovie
program Claerbout (1985) provides a laboratory for testing the new
algorithm.
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the results of the new extrapolation
procedure with the conventional Crank-Nicolson solution to the
45
compares the results of the new extrapolation
procedure with the conventional Crank-Nicolson solution to the
45![]() equation. The new approach has little dispersion since I
use a rational approximation (the `one-sixth trick') to the
Laplacian on the vertical and horizontal axes. In addition, the new
factorization retains accuracy up to 90
equation. The new approach has little dispersion since I
use a rational approximation (the `one-sixth trick') to the
Laplacian on the vertical and horizontal axes. In addition, the new
factorization retains accuracy up to 90![]() . The high dip,
evanescent energy in the 45
. The high dip,
evanescent energy in the 45![]() movie, propagates correctly in the
new approach.
movie, propagates correctly in the
new approach.
|
vs45
Figure 3 Comparison of the 45 |  |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
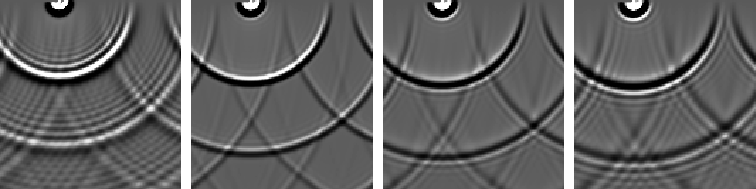
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares different value of the `one-sixth'
parameter,
compares different value of the `one-sixth'
parameter, ![]() . For this application, the optimal value seems to
be
. For this application, the optimal value seems to
be ![]() .
.
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)
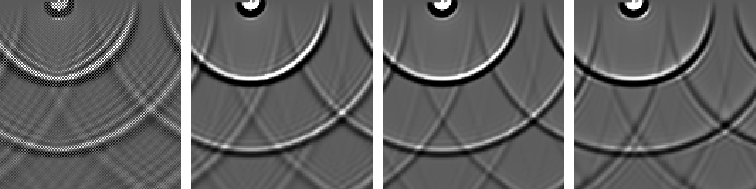
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares different finite-difference
Laplacian operators. In all cases the finite-difference Laplacian was
given by the linear sum of 5-point filters,
compares different finite-difference
Laplacian operators. In all cases the finite-difference Laplacian was
given by the linear sum of 5-point filters,
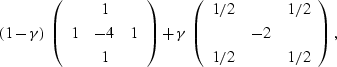 |
(33) |
 |
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)