




Next: Propagating waves with the
Up: The Helmholtz equation
Previous: The Helmholtz equation
The basis for wavefield extrapolation is an operator, R, that
marches the wavefield q, at depth z, down to depth 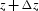 .
.
| 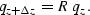 |
(28) |
In constant velocity, R will be a function of horizontal wavenumber,
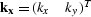 , and ideally,
, and ideally, 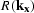 will have the form of the
phase-shift operator Gazdag (1978),
will have the form of the
phase-shift operator Gazdag (1978),
| 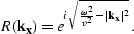 |
(29) |
Due to lateral velocity variations, and the desire to avoid spatial
Fourier transforms, approximations to R are often applied
in the 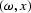 domain.
Typically R is split into a `thin-lens' term that propagates the
wave vertically, and a `diffraction' term that models more complex
wave phenomena. In the
domain.
Typically R is split into a `thin-lens' term that propagates the
wave vertically, and a `diffraction' term that models more complex
wave phenomena. In the 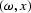 domain, the thin-lens term
can be applied as a simple phase-shift, while the diffraction term is
approximated by a small finite-difference filter. The method of
extrapolation determines the nature of the finite-difference
filter.
The mathematical forms of different extrapolators are summarized in
Table 1, and discussed below.
domain, the thin-lens term
can be applied as a simple phase-shift, while the diffraction term is
approximated by a small finite-difference filter. The method of
extrapolation determines the nature of the finite-difference
filter.
The mathematical forms of different extrapolators are summarized in
Table 1, and discussed below.
Table 3.1:
Comparison of the mathematical form of various wavefield
extrapolators.
| Gazdag: |
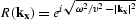 |
|---|
| Implicit: |
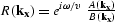 |
| Explicit: |
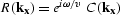 |
| Helmholtz factorization: |
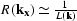 |
Implicit extrapolation (discussed in more detail in following
chapters) approximates 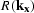 with a rational form,
consisting of a convolutional filter, and an inverse filter,
with a rational form,
consisting of a convolutional filter, and an inverse filter,
| 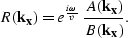 |
(30) |
In constant velocity, the traditional Crank-Nicolson implicit
formulation ensures the pair of convolutional operators, A
and B, are complex conjugates, and so the resulting
extrapolator is unitary.
Practical 3-D extrapolation is often done with an explicit operator
using McClellan transforms. This approach amounts to approximating
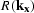 by with a simple convolutional filter,
by with a simple convolutional filter, 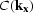 .Explicit extrapolators, therefore, have the form
.Explicit extrapolators, therefore, have the form
| 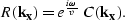 |
(31) |
In contrast to these methods, the minimum-phase factorization of the
Helmholtz operator provides a recursive depth
extrapolator of a different form:
| 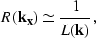 |
(32) |
where 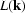 is a minimum-phase filter.
Because L is a function of
is a minimum-phase filter.
Because L is a function of 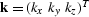 ,rather than
,rather than 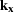 ,extrapolation with the Helmholtz factorization does not fit
exactly with equation (
,extrapolation with the Helmholtz factorization does not fit
exactly with equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
In practice the wavefield needs to be zero-padded in depth before
extrapolation, and so equation (
).
In practice the wavefield needs to be zero-padded in depth before
extrapolation, and so equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is not written
as an equality.
) is not written
as an equality.
The apparent contradiction that we are approximating the
unitary (delay) operator in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the
minimum-phase extrapolator in equation (
) with the
minimum-phase extrapolator in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
resolved by examining the impulse response of the operator
) is
resolved by examining the impulse response of the operator
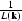 shown in Figure
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The impulse response consists of two `bumps'.
The first bump is the response of the impulse at the same depth step
as the impulse.
Because it looks like a delta function, it leaves that depth step
essentially unchanged.
The second bump, on the other hand, is the response to the impulse at
the following depth step -- it describes the wave propagation in
depth.
When taken together, the first and second bumps are indeed minimum
phase; however, the second bump controls wave propagation in depth and
is almost pure delay.
.
The impulse response consists of two `bumps'.
The first bump is the response of the impulse at the same depth step
as the impulse.
Because it looks like a delta function, it leaves that depth step
essentially unchanged.
The second bump, on the other hand, is the response to the impulse at
the following depth step -- it describes the wave propagation in
depth.
When taken together, the first and second bumps are indeed minimum
phase; however, the second bump controls wave propagation in depth and
is almost pure delay.
impresp
Figure 2 Amplitude of impulse response of
polynomial division with minimum-phase factorization of the Helmholtz
equation. The top panel shows the location of the impulse. The bottom
panel shows the impulse response. Helical boundary conditions mean
the second bump in the impulse response corresponds to energy
propagating to the next depth step.
|
|  |










Next: Propagating waves with the
Up: The Helmholtz equation
Previous: The Helmholtz equation
Stanford Exploration Project
5/27/2001
![]() domain.
Typically R is split into a `thin-lens' term that propagates the
wave vertically, and a `diffraction' term that models more complex
wave phenomena. In the
domain.
Typically R is split into a `thin-lens' term that propagates the
wave vertically, and a `diffraction' term that models more complex
wave phenomena. In the ![]() domain, the thin-lens term
can be applied as a simple phase-shift, while the diffraction term is
approximated by a small finite-difference filter. The method of
extrapolation determines the nature of the finite-difference
filter.
The mathematical forms of different extrapolators are summarized in
Table 1, and discussed below.
domain, the thin-lens term
can be applied as a simple phase-shift, while the diffraction term is
approximated by a small finite-difference filter. The method of
extrapolation determines the nature of the finite-difference
filter.
The mathematical forms of different extrapolators are summarized in
Table 1, and discussed below.
![]() with a rational form,
consisting of a convolutional filter, and an inverse filter,
with a rational form,
consisting of a convolutional filter, and an inverse filter,
![]() by with a simple convolutional filter,
by with a simple convolutional filter, ![]() .Explicit extrapolators, therefore, have the form
.Explicit extrapolators, therefore, have the form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
In practice the wavefield needs to be zero-padded in depth before
extrapolation, and so equation (
).
In practice the wavefield needs to be zero-padded in depth before
extrapolation, and so equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is not written
as an equality.
) is not written
as an equality.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the
minimum-phase extrapolator in equation (
) with the
minimum-phase extrapolator in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
resolved by examining the impulse response of the operator
) is
resolved by examining the impulse response of the operator
![]() shown in Figure
shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
The impulse response consists of two `bumps'.
The first bump is the response of the impulse at the same depth step
as the impulse.
Because it looks like a delta function, it leaves that depth step
essentially unchanged.
The second bump, on the other hand, is the response to the impulse at
the following depth step -- it describes the wave propagation in
depth.
When taken together, the first and second bumps are indeed minimum
phase; however, the second bump controls wave propagation in depth and
is almost pure delay.
.
The impulse response consists of two `bumps'.
The first bump is the response of the impulse at the same depth step
as the impulse.
Because it looks like a delta function, it leaves that depth step
essentially unchanged.
The second bump, on the other hand, is the response to the impulse at
the following depth step -- it describes the wave propagation in
depth.
When taken together, the first and second bumps are indeed minimum
phase; however, the second bump controls wave propagation in depth and
is almost pure delay.
