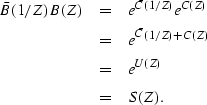Next: Multi-dimensional factorization
Up: Model of stochastic oscillations
Previous: Model of stochastic oscillations
Kolmogorov 1939 spectral factorization provides a highly
efficient Fourier method for calculating a minimum phase time domain
function with a given power spectrum. The Kolmogorov spectral
factorization method is commonly referred to as the Hilbert transform
method within the signal processing community
[e.g. Robinson and Treitel (1980)],
although they are equivalent.
Following Claerbout 1992,
we will describe the method briefly with Z transform notation.
In this notation, 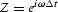 is the unit delay
operator, and functions can be evaluated either in the frequency
domain as functions of
is the unit delay
operator, and functions can be evaluated either in the frequency
domain as functions of  , or in the time domain as the
coefficients of the polynomial in Z.
Causal functions can, therefore, be written as polynomials with
non-negative powers of Z, whereas anti-causal functions contain
non-positive powers of Z.
, or in the time domain as the
coefficients of the polynomial in Z.
Causal functions can, therefore, be written as polynomials with
non-negative powers of Z, whereas anti-causal functions contain
non-positive powers of Z.
The spectral factorization problem can be summarized as given a power
spectrum, S(Z), we must find a minimum phase function such that
| 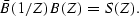 |
(3) |
Since S(Z) is a power spectrum, it is non-negative by definition for
all  ; however, the Kolmogorov process places the additional
requirement that S(Z) contains no zeros. If this is the case, then we
can safely take its logarithm,
; however, the Kolmogorov process places the additional
requirement that S(Z) contains no zeros. If this is the case, then we
can safely take its logarithm,
| ![\begin{displaymath}
U(\omega)=\ln \left[ S(\omega) \right].\end{displaymath}](img15.gif) |
(4) |
Since 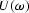 is real and even, its time domain representation is
also real and even. We can therefore isolate its causal part,
C(Z), and its anti-causal part,
is real and even, its time domain representation is
also real and even. We can therefore isolate its causal part,
C(Z), and its anti-causal part, 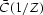 :
:
| 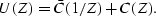 |
(5) |
Once we have C(Z), we can easily obtain B(Z) through
| 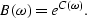 |
(6) |
To verify that B(Z) of this form does indeed satisfy
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), consider
), consider
| 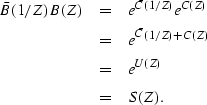 |
(7) |
| (8) |
| (9) |
| (10) |
B(Z) will be causal since C(Z) was causal, and a power series
expansion proves that the exponential of a causal function is also
causal. It is also clear that 1/B(Z)=e-C(Z) will also be causal
in the time domain. Therefore, B(Z) will be causal, and will have a
causal inverse. Hence B(Z) satisfies the definition of minimum phase
given above.





Next: Multi-dimensional factorization
Up: Model of stochastic oscillations
Previous: Model of stochastic oscillations
Stanford Exploration Project
5/27/2001
![]() is the unit delay
operator, and functions can be evaluated either in the frequency
domain as functions of
is the unit delay
operator, and functions can be evaluated either in the frequency
domain as functions of ![]() , or in the time domain as the
coefficients of the polynomial in Z.
Causal functions can, therefore, be written as polynomials with
non-negative powers of Z, whereas anti-causal functions contain
non-positive powers of Z.
, or in the time domain as the
coefficients of the polynomial in Z.
Causal functions can, therefore, be written as polynomials with
non-negative powers of Z, whereas anti-causal functions contain
non-positive powers of Z.
![]() ; however, the Kolmogorov process places the additional
requirement that S(Z) contains no zeros. If this is the case, then we
can safely take its logarithm,
; however, the Kolmogorov process places the additional
requirement that S(Z) contains no zeros. If this is the case, then we
can safely take its logarithm,
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), consider
), consider