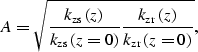Next: Applications of amplitude-preserved migration
Up: Modeling and migration amplitudes
Previous: Amplitude correction in constant
The results presented in the preceding subsection are strictly valid in
constant velocity. When velocity varies, the propagation operator
(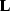 ) is not only a constant magnitude phase-shift
multiplication, but also includes an amplitude term
that changes with depth and horizontal location.
Therefore, the integrals in Equation (5) cannot be
interpreted as Fourier transforms anymore.
Clayton and Stolt (1981) show how this issue can be theoretically
side-stepped by datuming the data just above each reflector,
and by approximating the velocity as constant in the imaging interval.
In practice, this issue is taken care of by evaluating
the Jacobian and the reflection operator G,
using the local velocity at the imaging location.
) is not only a constant magnitude phase-shift
multiplication, but also includes an amplitude term
that changes with depth and horizontal location.
Therefore, the integrals in Equation (5) cannot be
interpreted as Fourier transforms anymore.
Clayton and Stolt (1981) show how this issue can be theoretically
side-stepped by datuming the data just above each reflector,
and by approximating the velocity as constant in the imaging interval.
In practice, this issue is taken care of by evaluating
the Jacobian and the reflection operator G,
using the local velocity at the imaging location.
When the continuation equation includes the amplitude term (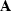 ),
Equation (7) becomes
),
Equation (7) becomes
| 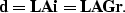 |
(9) |
Since conventional migration is the adjoint of modeling,
Equation (8) becomes
| 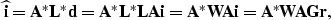 |
(10) |
In layered media, the frequency-wavenumber amplitude term of the
continuation operator can be computed using the WKBJ approximation
as a diagonal real operator Clayton and Stolt (1981):
| 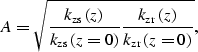 |
(11) |
where 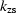 and
and 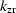 are the depth wavenumbers associated with source
and receiver.
are the depth wavenumbers associated with source
and receiver.





Next: Applications of amplitude-preserved migration
Up: Modeling and migration amplitudes
Previous: Amplitude correction in constant
Stanford Exploration Project
4/30/2001
![]() ),
Equation (7) becomes
),
Equation (7) becomes