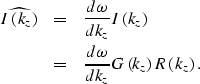Next: Amplitude correction in variable
Up: Modeling and migration amplitudes
Previous: Modeling and migration amplitudes
Migration is, by the standard definition, the operation adjoint to
forward modeling.
It is performed by the downward continuing the recorded wavefield
and imaging at zero time:
| 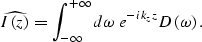 |
(3) |
We substitute Equation (1) into
Equation (3), and expand
the integral in Equation (1)
to negative depth, for which the image is zero, by definition:
| 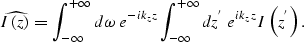 |
(4) |
We then change the integration variable 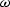 to kz and obtain:
to kz and obtain:
| 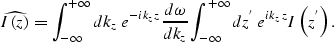 |
(5) |
The pair of integrals in Equation (5)
describe forward and inverse Fourier transforms,
and thus the effect of chaining modeling and migration
on the image is simply the equivalent of applying
the Jacobian 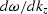 .This result is valid only for real values of kz, which is
what we want, since we are not interested in the wavefield
component for which kz becomes imaginary
(that is, we neglect evanescent waves).
.This result is valid only for real values of kz, which is
what we want, since we are not interested in the wavefield
component for which kz becomes imaginary
(that is, we neglect evanescent waves).
In constant velocity, the frequency-wavenumber representation of the
Jacobian is simply a multiplication:
| 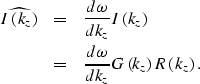 |
|
| (6) |
The Jacobian weighting is introduced by the imaging step,
therefore, the Jacobian depends on the coordinates used to define
the wavefield during imaging: constant ray-parameter
or constant offset wavenumber.
In matrix notation, Equation (1) is written
| 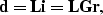 |
(7) |
where 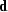 ,
, 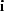 , and
, and  are respectively
the data, image, and reflectivity vectors,
are respectively
the data, image, and reflectivity vectors,
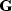 is a diagonal matrix representing the reflection operator,
and
is a diagonal matrix representing the reflection operator,
and 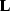 is the modeling operator.
With this notation, Equation (5) becomes
is the modeling operator.
With this notation, Equation (5) becomes
| 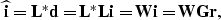 |
(8) |
where 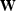 is a diagonal matrix representing the Jacobian
is a diagonal matrix representing the Jacobian
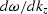 .
.





Next: Amplitude correction in variable
Up: Modeling and migration amplitudes
Previous: Modeling and migration amplitudes
Stanford Exploration Project
4/30/2001
![]() .This result is valid only for real values of kz, which is
what we want, since we are not interested in the wavefield
component for which kz becomes imaginary
(that is, we neglect evanescent waves).
.This result is valid only for real values of kz, which is
what we want, since we are not interested in the wavefield
component for which kz becomes imaginary
(that is, we neglect evanescent waves).