Modeling and migration amplitudes

This section sets the general framework of amplitude analysis and correction in relation to wave-equation modeling and migration.

The data (D) recorded at the surface can be modeled from the image (I) by integrating over depth (z) all the contributions of the reflected wavefield  

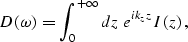$$D\left (\omega\right )= \int_{0}^{+\infty} dz\; e^{ik_zz} I\left (z \right ),$$ (1)

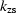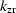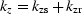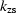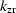where the vertical wavenumber (k_z), given by the double square root (DSR) equation, is the sum of two components: ${k_{\rm zs}}$ for continuing the sources, and ${k_{\rm zr}}$ for continuing the receivers ($k_z={k_{\rm zs}}+{k_{\rm zr}}$). The expressions for ${k_{\rm zs}}$ and ${k_{\rm zr}}$depend on the migration type and CIG type. However, the discussion in this section is general and independent of the particular expressions for 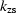${k_{\rm zs}}$ and ${k_{\rm zr}}$.

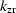The image is linked to physical parameters, such as reflectivity (R), by a reflection operator (G) that relates the upgoing wavefield, to the downgoing wavefield, such that I=GR. The form of this reflection, or scattering, operator depends on the physical model adopted for the reflection process.

In the case of constant velocity, for which we can use the definitions introduced by Clayton and Stolt (1981) and Stolt and Benson (1986), the operator (G) is a simple frequency-wavenumber domain multiplication defined by  

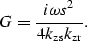$$G= \frac{i \omega s^2}{4 {k_{\rm zs}}{k_{\rm zr}}}.$$ (2)