




Next: Estimating and Handling Random
Up: Least Squares Formulation
Previous: Least Squares Formulation
In many applications, the interval velocity must be smooth across layer
boundaries. To accomplish this, we incorporate a penalty on the change
in velocity across the layer boundary, and effectively exchange quality in
data fit for a continuous result.
However, as mentioned by Lizarralde and Swift (1999), an accumulation of
large residual errors would result if we forced continuity in the velocity
function across layer boundaries with large velocity contrast. Therefore we
``turn off'' the discontinuity penalty at certain layers via a user-defined
``hard rock'' weight.
Let us write the weighted discontinuity penalty at the boundary between layers
l and l+1:
| ![\begin{displaymath}
w^h_l \left[ v_{0,l} + k_l t_l - \left(v_{0,l+1} + k_{l+1}t_l \right) \right]\end{displaymath}](img15.gif) |
(6) |
whl is the hard rock weight. We suggest that the whl be treated as
a binary quantity: either 1 for soft rock boundaries or 0 for hard rock
boundaries. As before, we write the misfits of equation (6)
in fitting goal notation and combine with equation (5):
| ![\begin{displaymath}
\left[\begin{array}
{c}
\bold A \\ \epsilon \bold C
\end{...
...n{array}
{c}
\boldsymbol \zeta \\ \bold 0
\end{array}\right]\end{displaymath}](img16.gif) |
(7) |
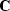 is simply the linear operator suggested by equation (6):
a matrix with coefficients of
is simply the linear operator suggested by equation (6):
a matrix with coefficients of 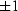 and
and 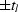 , with rows weighted by
the whl. Application of
, with rows weighted by
the whl. Application of 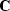 is tantamount to applying a scaled,
discrete first derivative operator to the model parameters in time.
The scalar
is tantamount to applying a scaled,
discrete first derivative operator to the model parameters in time.
The scalar  controls the trade off between model continuity and
data fitting. Lizarralde and Swift (1999) give a detailed strategy for
choosing
controls the trade off between model continuity and
data fitting. Lizarralde and Swift (1999) give a detailed strategy for
choosing  .
.





Next: Estimating and Handling Random
Up: Least Squares Formulation
Previous: Least Squares Formulation
Stanford Exploration Project
4/29/2001