Choice of $\epsilon$ and number of CG iterations

In principle, the number of iterations should not be an important parameter since we should iterate until the solution converges. However, determining the correct value of $\epsilon$ is a long-standing difficulty with large exploration-type geophysical inverse problems. Conventional solutions Menke (1989) such as picking the knee of misfit vs. model norm curves, or examining the singular-values of the operator matrix are not practical when the model-space is a large multi-dimensional image. If the choice of $\epsilon$ is too small, the solution will begin to degrade as the number of iterations increases as poorly resolved eigenvectors leak into the model space. On the other hand, if the choice of $\epsilon$ is too large, the solution will converge to a smooth model that does not satisfy our first fitting goal [expression (7)].

Despite these difficulties, with preconditioned problems we often obtain good results after only a few iterations without the solution fully converging, and with little or no dependence on the the choice of $\epsilon$. Well-resolved low-frequency eigenvectors propagate into the solution quickly after only a few iterations.

Therefore, to reduce the dimensionality of the parameter space, we set 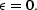$\epsilon=0.$, and keep the filters smooth by restricting the number of conjugate-gradient iterations Crawley (1999). After solving the problem only once, we can plot misfit vs. model norm curves for intermediate solutions with varying number of iterations, and choose the best result.