




Next: Choice of non-stationary shaping-filter
Up: Parameter choices
Previous: Choice of and number
The most important consideration in the choice of roughening filter is
that it is easily invertible. A Fourier domain roughener would meet
this criterion; however, we apply a time-space operator that is both
cheaper, and less prone to Fourier artifacts such as wrap-around and
Gibbs' phenomenom.
Claerbout (1998b) describes how to construct invertible
multi-dimensional time-space operators by applying helical boundary
conditions to the problem. Helical operators cost O(N) operations
to apply and invert rather than 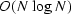 for an equivalent
Fourier operator.
for an equivalent
Fourier operator.
For the results shown in this paper, we choose 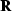 to be the
helical derivative operator that roughens
isotropically in the midpoint-time plane. A cascade of two
one-dimensional derivative filters first along the time axis and then
along the midpoint axis also works well.
Anisotropic smoothing can be controlled by tweaking the ``micropatch''
parameters described below.
to be the
helical derivative operator that roughens
isotropically in the midpoint-time plane. A cascade of two
one-dimensional derivative filters first along the time axis and then
along the midpoint axis also works well.
Anisotropic smoothing can be controlled by tweaking the ``micropatch''
parameters described below.





Next: Choice of non-stationary shaping-filter
Up: Parameter choices
Previous: Choice of and number
Stanford Exploration Project
4/29/2001
![]() to be the
helical derivative operator that roughens
isotropically in the midpoint-time plane. A cascade of two
one-dimensional derivative filters first along the time axis and then
along the midpoint axis also works well.
Anisotropic smoothing can be controlled by tweaking the ``micropatch''
parameters described below.
to be the
helical derivative operator that roughens
isotropically in the midpoint-time plane. A cascade of two
one-dimensional derivative filters first along the time axis and then
along the midpoint axis also works well.
Anisotropic smoothing can be controlled by tweaking the ``micropatch''
parameters described below.