Kinematics of common-azimuth migration are only approximately
correct when the velocity varies.
The errors are related to the departure of
the reflected events wavepaths
from the common-azimuth geometry.
This phenomenon can be easily understood
by analyzing the raypaths of reflections.
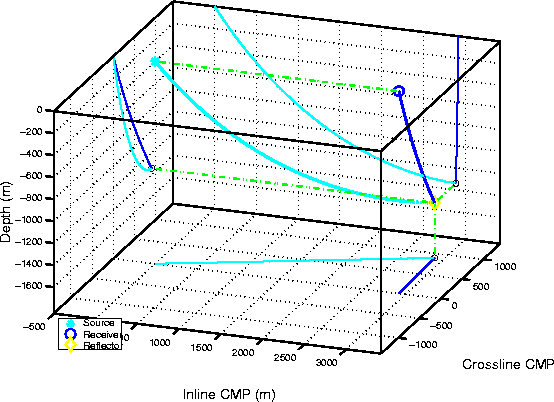
Figure 1 shows an example
of raypaths for an event bouncing off
a reflector dipping at 60 degrees
and oriented at 45 degrees with respect to the offset direction.
The offset is equal to 2.9 km,
and the velocity function is ![]() km/s.
The projections of the rays on the crossline plane
clearly show the raypaths departure from
the common-azimuth geometry.
Notice that the source ray (light gray) is close to overturn.
A dipping reflector oriented at 45 degrees
with rays close to overturn is the worst-case scenario
for common-azimuth migration.
km/s.
The projections of the rays on the crossline plane
clearly show the raypaths departure from
the common-azimuth geometry.
Notice that the source ray (light gray) is close to overturn.
A dipping reflector oriented at 45 degrees
with rays close to overturn is the worst-case scenario
for common-azimuth migration.
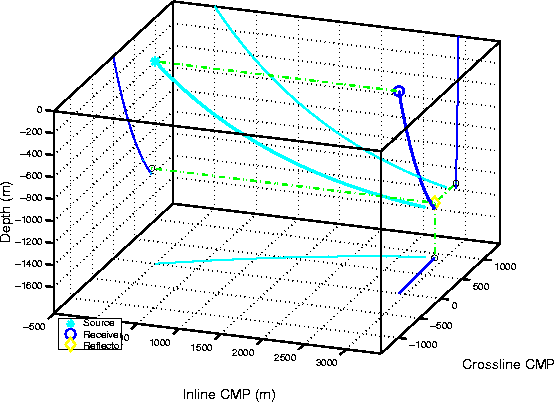
The event modeled with raytracing can also be imaged using raytracing by a simple process that I will identify as raytracing migration. Starting from the initial conditions at the surface given by modeling, both the shot and the receiver rays are traced downward until the sum of their traveltimes is equal to the traveltime of the reflected event. When raytracing migration is performed using the exact equation derived from an asymptotic approximation of the double-square root equation, the rays are exactly the same as the rays shown in Figure 1. On the contrary, if the common-azimuth approximation is introduced in the raytracing equations, the rays will follow the paths shown in Figure 2. As expected, the projections of the rays on the crossline plane overlap perfectly, confirming that the rays follow a common-azimuth geometry. However, in Figure 2 it is also apparent that the common-azimuth rays do not meet at the ending points. This discrepancy in the kinematics causes errors in the migration.
 |
 |
To connect the kinematic analysis
with migration errors,
I migrated
a data set with similar characteristics
as the events analyzed above.
This data set was created by Louis Vaillant
Vaillant and Biondi (2000).
Data were generated using SEPlib Kirmod3d program.
The reflectivity field consists of a set of five dipping planes,
from zero dip to 60 degrees dip.
The azimuth of the planes is 45 degrees
with respect to the direction of the acquisition.
The velocity was ![]() km/s,
which roughly corresponds to typical gradients found in the Gulf of Mexico.
The maximum source-receiver offset was 3 km.
Figure 3 shows the geometry of the reflectors.
km/s,
which roughly corresponds to typical gradients found in the Gulf of Mexico.
The maximum source-receiver offset was 3 km.
Figure 3 shows the geometry of the reflectors.
|
planes
Figure 3 Geometry of the set of slanted planes, dipping at | 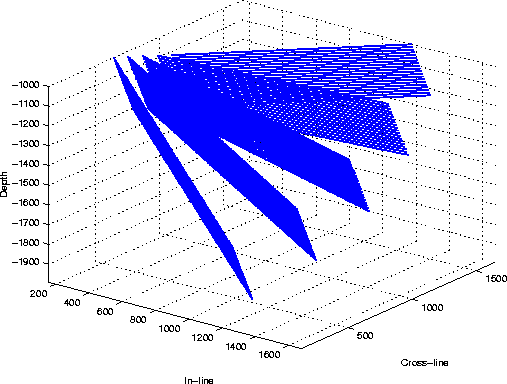 |
Figure 4 shows a subset of the migration results. The front face of the cube displayed in the figure is an inline section through the stack. The other two faces are sections through the prestack image as a function of the offset ray parameter pxh. This migration results were obtained by including all the appropriate weighting factors, as discussed by Sava and Biondi 2001, including the phase shift and weights related to the stationary phase approximation.
Figure 5
shows an individual ADCIG gather from the same migrated
image shown
in Figure 4.
The three events in the figure correspond to the
planes dipping at 30, 45 and 60 degrees.
Notice that the events are almost perfectly flat
as a function of the offset ray parameter pxh,
except for the reflections from
the 60 degrees dipping plane
with large offset ray parameters
(i.e. large reflection angle).
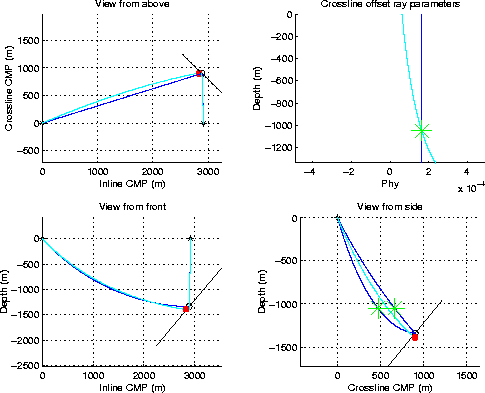
Figures 1- 2 show
the rays corresponding to one of these events;
in particular the one corresponding to
pxh=.00045 s/m.
Figure 6 shows the three
orthogonal projections of these rays.
The black (blue in colors) rays are the exact rays,
while the light gray (cyan in colors)
rays are the common-azimuth rays for the
same events recorded at the surface.
The solid (red in colors) dot corresponds to the imaging location
for the common-azimuth migration.
It is at the midpoint between the end points of the two rays.
It is deeper than the correct one
by ![]() =48 m,
and laterally shifted by
=48 m,
and laterally shifted by
![]() =-56 m and
=-56 m and
![]() =-2 m.
However,
at fixed horizontal location,
the dot is shallower by
=-2 m.
However,
at fixed horizontal location,
the dot is shallower by
![]() =-21 m than the reflecting plane.
This is about the same vertical shift that is observable
on the corresponding event in the ADCIG gather shown in
Figure 5.
=-21 m than the reflecting plane.
This is about the same vertical shift that is observable
on the corresponding event in the ADCIG gather shown in
Figure 5.
The maximum crossline offset of the exact rays is about 200 m. This maximum offset occurs at the intersection between the crossline offset ray parameter (pyh) curves shown on the top-right panel in Figure 6. This small value for the maximum crossline offset, compared with the inline offset, suggests the that event could be exactly downward continued by expanding the computational domain in a narrow strip around the zero crossline offset. However, to minimize the number of crossline offsets needed to adequately sample the crossline-offset dips (pyh), it is important to define an optimal range of pyh that is not symmetric around the origin. In the next section I will discuss how to use the common-azimuth migration equations for defining such a range.
To evaluate the importance of not centering the range of
pyh at zero,
I migrated the data assuming pyh=0 for all events,
and I also performed the corresponding raytracing migration.
Figure 7
shows the same ADCIG gather as
in Figure 5,
but extracted from the image obtained assuming pyh=0.
In this gather the events are significantly
frowning down.
Furthermore, no image is present for the larger pxh.
For example, the deeper reflector is not imaged
at the ray parameter corresponding
to the event represented in
Figures 1- 2
(pxh=.00045 s/m).
The lack of images is readily explained with raytracing.
If the condition pyh=0
is introduced in the raytracing equations
one of the rays tends to overturn shallower
than the true rays.
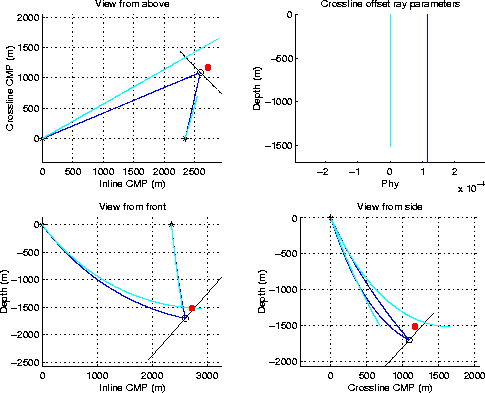
Figure 8 shows
the raytracing migration corresponding to pxh=.000325 s/m,
one of the larger values of pxh for which an event
could be raytraced without neither of the rays overturning.
The rays traced assuming pyh=0 (light-gray lines)
are clearly far from the correct rays (black lines).
Figure 9 shows the corresponding
common-azimuth raytracing migration for the same event (pxh=.000325 s/m)
and offset 2.35 km.
As for Figure 1,
the solid dot corresponds to the imaging location
for the common-azimuth migration.
For common-azimuth migration the
errors are much smaller than for pyh=0,
and about half than in Figure 6.
The dot is deeper than the correct one
by ![]() =22 m,
and laterally shifted by
=22 m,
and laterally shifted by
![]() =-23 m and
=-23 m and
![]() =-4 m.
At fixed horizontal location,
the dot is shallower by
=-4 m.
At fixed horizontal location,
the dot is shallower by
![]() =-9 m than the reflecting plane.
This is about the same vertical shift observable
on the corresponding event in the ADCIG gather shown in
Figure 5.
=-9 m than the reflecting plane.
This is about the same vertical shift observable
on the corresponding event in the ADCIG gather shown in
Figure 5.
|
CA-pull-WKBJ-stat-vp
Figure 4 Subset of the results of common-azimuth migration of the synthetic data set. The front face of the cube is an inline section through the stack. The other two faces are sections through the prestack image. This migration results were obtained by including all the appropriate weighting factors, including the phase shift and weights related to the stationary phase approximation. | 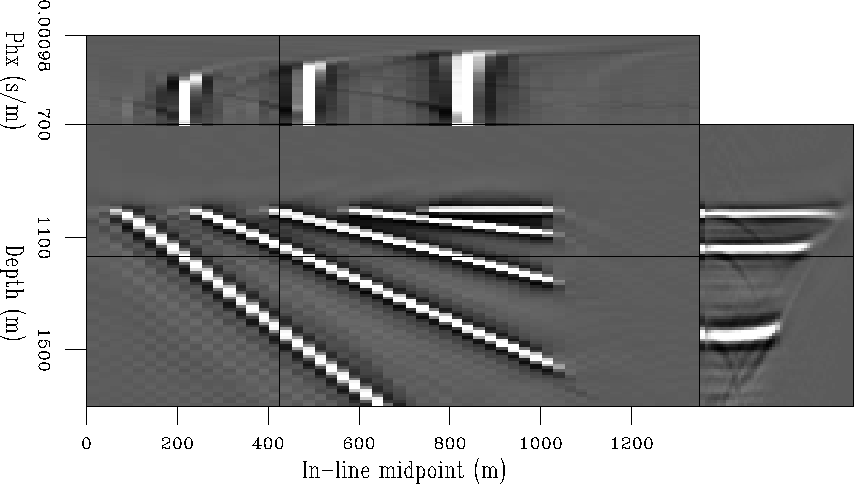 |
|
CIG-CA-pull-WKBJ-stat-cig
Figure 5 An ADCIG extracted from the same migrated image shown in Figure 4. The three events in the figure correspond to the planes dipping at 30, 45 and 60 degrees. Notice that the events are almost perfectly flat except for the large offset ray parameters (i.e. large reflection angle) of the 60 degrees dipping plane. | 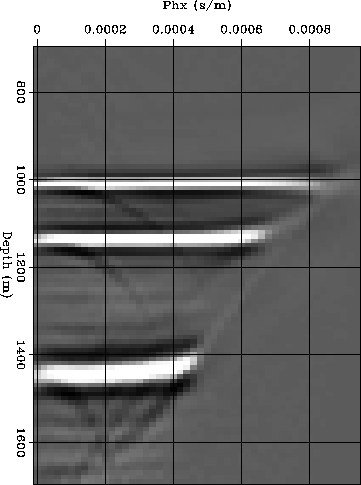 |
 |
|
CIG-PS-1-nhy-WKBJ-stat-cig
Figure 7 An ADCIG extracted from the migrated image obtained by assuming pyh=0 during downward continuation. The three events in the figure correspond to the planes dipping at 30, 45 and 60 degrees. Notice that the events are frowning down and that no image is present at large ray parameters. | 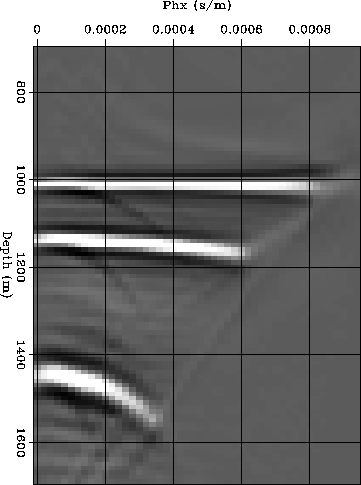 |
 |
 |