




Next: Migration tests
Up: Biondi: Narrow-azimuth migration
Previous: Analysis of common-azimuth migration
The kinematic analysis presented in the previous section
suggests a generalization of common-azimuth migration
based on the downward continuation
of a narrow strip around the zero crossline offset.
The computational cost of such a generalization
is obviously proportional to the number of crossline
offsets used to represent this narrow strip.
The width of the strip is dependent on the
reflector geometry and on the velocity model,
but the sampling depends on the crossline-offset
dip spectrum.
To minimize the cost it is crucial
to define an optimal criterion to define
the range of crossline-offset dips (pyh).
As demonstrated in the previous section,
for dipping reflectors
the dip spectrum is not centered around
the zero dip (pyh=0),
and thus a symmetric range would be
wasteful.
I exploit the information provided by the common-azimuth
equation to define a range of crossline-offset dips.
For this reason I named my generalization narrow-azimuth
migration,
even if narrow crossline-offset would be
a more accurate name.
The common-azimuth equation
provides the crossline-offset dip pyh
as a function of the other dips in the data
when the data are propagated along a constant azimuth
Biondi and Palacharla (1996).
In the frequency-wavenumber domain
the common-azimuth relationship
is:
| 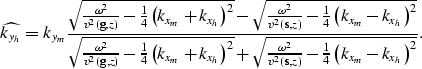 |
(1) |
where
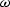 is the temporal frequency,
kxm and kym are the midpoint wavenumbers,
kxh and kyh are the offset wavenumbers,
and
is the temporal frequency,
kxm and kym are the midpoint wavenumbers,
kxh and kyh are the offset wavenumbers,
and 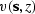 and
and 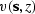 are the local velocities.
Ideally we would like to define a range of kyh
that is varying with depth, as a function of
the local velocities.
However, that may lead to complex implementation.
For the moment I chose a simpler solution.
I define a range of kyh
by setting a minimum velocity
are the local velocities.
Ideally we would like to define a range of kyh
that is varying with depth, as a function of
the local velocities.
However, that may lead to complex implementation.
For the moment I chose a simpler solution.
I define a range of kyh
by setting a minimum velocity 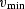 and a maximum velocity
and a maximum velocity 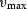 ,and define
,and define
| 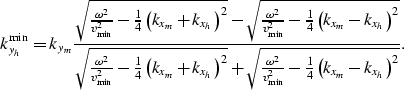 |
(2) |
and
| 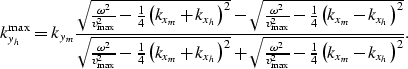 |
(3) |
The disadvantage of this solution is that the choice of
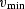 and
and 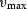 is somewhat arbitrary.
is somewhat arbitrary.
The central point of the kyh range is then defined
as a function of 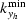 and
and 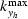 as
as
| 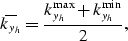 |
(4) |
and the range as
| 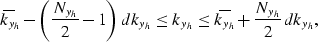 |
(5) |
where Nyh is the number of crossline offsets
and dkyh is the sampling in kyh.
The two narrow azimuth schemes that I propose and
tested differ in the definition of the crossline-offset
wavenumber sampling dkyh.
The first, and simplest, uses a constant
value for dkyh;
that is
| 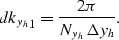 |
(6) |
The second one allows dkyh to vary as
| 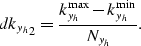 |
(7) |
Varying dkyh
is equivalent to vary the width of the crossline-offset strip,
and, at constant Nyh,
is also equivalent to vary the sampling 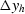 .At lower frequencies dkyh is smaller,
and thus the maximum crossline offset is larger.
The migrated results benefit
because the lower frequencies are the most affected
by boundary artifacts and
a wider strip reduces the artifacts
caused by the boundaries.
On the contrary, as the frequency increases,
dkyh is larger and
.At lower frequencies dkyh is smaller,
and thus the maximum crossline offset is larger.
The migrated results benefit
because the lower frequencies are the most affected
by boundary artifacts and
a wider strip reduces the artifacts
caused by the boundaries.
On the contrary, as the frequency increases,
dkyh is larger and
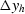 smaller,
and thus spatial aliasing is avoided.
smaller,
and thus spatial aliasing is avoided.
The main disadvantage of this second scheme
is that the transformation between space
and wavenumber domains becomes more cumbersome.
Mixed space/wavenumber domain downward-continuation methods
Biondi (1999) become more expensive,
and thus the scheme becomes less attractive
when the velocity is laterally varying.





Next: Migration tests
Up: Biondi: Narrow-azimuth migration
Previous: Analysis of common-azimuth migration
Stanford Exploration Project
4/29/2001
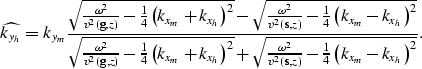
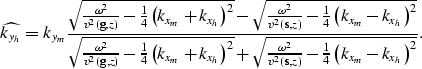
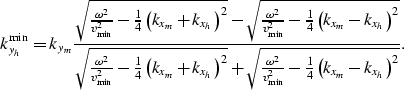
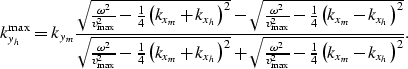
![]() and
and ![]() as
as