Next: Antialiasing conditions for the
Up: antialiasing the parabolic radon
Previous: antialiasing the parabolic radon
Prior to the dip filtering, however, it is necessary to compute
the PRT in the Fourier domain, rather than in the time domain.
The equations that follow show a method for computing the PRT
in the frequency domain. In the time domain, the equation for
a parabola is
| 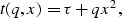 |
(1) |
where  is the zero offset time, x the offset, and q the
curvature of the parabola. The modeling equation, which
superposes on parabolas, from the radon domain to the CMP domain
is
is the zero offset time, x the offset, and q the
curvature of the parabola. The modeling equation, which
superposes on parabolas, from the radon domain to the CMP domain
is
| 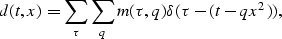 |
(2) |
and the adjoint transform, which sums along parabolas, is
| 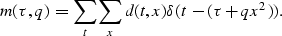 |
(3) |
We can easily transform these equations in the Fourier domain as follows:
| 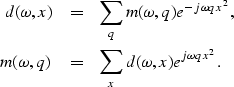 |
(4) |
| (5) |
With 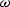 constant, equations (4) and (5) describe a simple matrix
multiplication with the operator
constant, equations (4) and (5) describe a simple matrix
multiplication with the operator 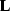 :
:
| 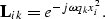 |
(6) |
Hence, we can write equations (4) and (5) in the following more
familiar way for each frequency:
| 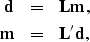 |
(7) |
| (8) |
where 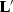 is the adjoint of
is the adjoint of 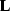 . I have computed the
radon and offset domains in Figure 2 using equations
(7) and (8). The following is a possible algorithm for
computing the radon domain:
. I have computed the
radon and offset domains in Figure 2 using equations
(7) and (8). The following is a possible algorithm for
computing the radon domain:

- Fourier transform the data.

- For each frequency, starting from the lowest to the
highest, solve equation (8).

- Inverse Fourier transform
 .
.
Because we can compute a pseudo-inverse for L noniteratively in the
Fourier domain Kostov (1989), the PRT is generally not
computed in the time domain.





Next: Antialiasing conditions for the
Up: antialiasing the parabolic radon
Previous: antialiasing the parabolic radon
Stanford Exploration Project
4/29/2001