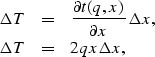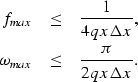Next: Operator antialiasing and least-squares
Up: antialiasing the parabolic radon
Previous: Computing the PRT in
Antialiasing the operator is equivalent to dip-filtering the operator.
The anti-aliasing conditions can be written Abma et al. (1999) as
| 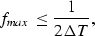 |
(9) |
where 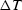 is the local slope of the operator between two adjacent
traces. For the PRT, we can compute the local slope as follows:
is the local slope of the operator between two adjacent
traces. For the PRT, we can compute the local slope as follows:
| 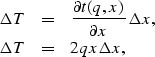 |
(10) |
| (11) |
where 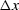 is the input trace spacing. The antialiasing condition becomes
is the input trace spacing. The antialiasing condition becomes
| 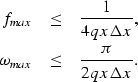 |
(12) |
| (13) |
The antialiasing condition in equation (13)
is then implemented in the Fourier domain.
Figure 3 shows how the antialiasing
works in the data space when the adjoint of the PRT (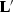 )
is applied to the model in Figure 1: parabolas
broaden with offset as a result of the dip filtering. Thus,
the antialiasing operator generates a loss of resolution.
)
is applied to the model in Figure 1: parabolas
broaden with offset as a result of the dip filtering. Thus,
the antialiasing operator generates a loss of resolution.
data_spikena
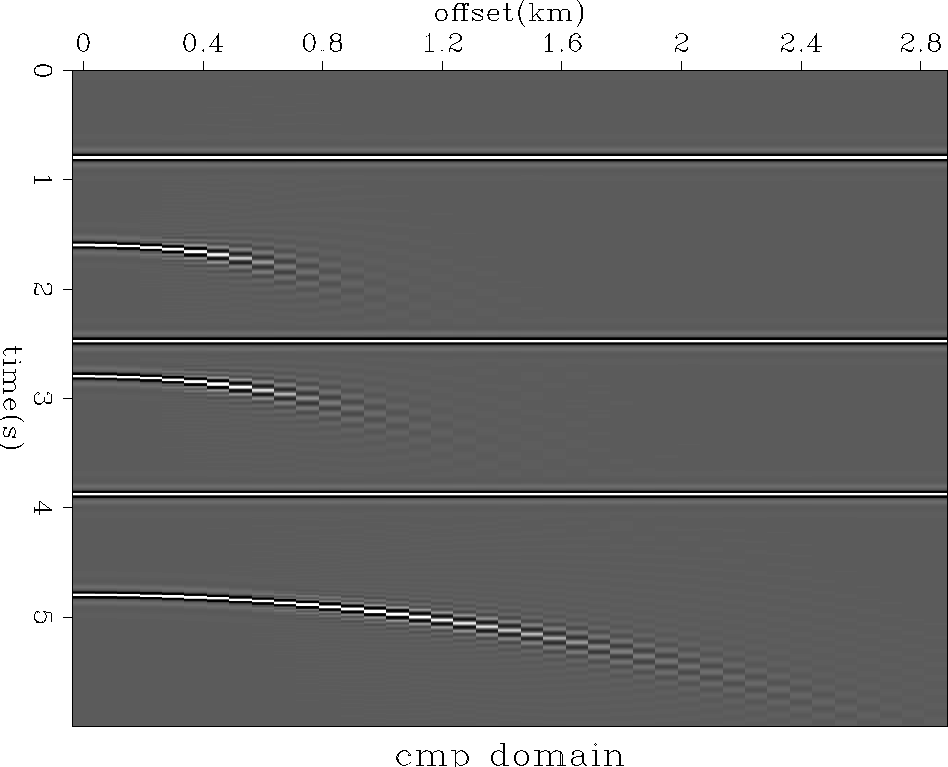
Figure 3 Effects of antialiasing
in the data space. The parabolas broaden with offset as a result of
the low-pass filtering for large qs.
|
|  |





We now apply the antialiasing operator to the CMP gather shown in the
right-hand panel of Figure 1.
The radon domain in Figure 4 (as compared with that
in Figure 2) has been cleaned up with a loss of
resolution. However,
because we apply an antialiasing operator with aliased data, we are
left with aliasing noise near q=0 s/km2. This aliasing noise is
caused by the aliasing of the non-flat events in the CMP domain.
We can mitigate these artifacts by introducing some constraints
in the radon domain as a function of the
expected aliased dips in the data Biondi (1998), but
this is not considered here. Nonetheless, we see that the use of an antialiasing
operator with aliased data is worthwhile. In addition, cleaning up the aliasing
artifacts for a high q is particularly interesting when multiples
are present in the data.
Indeed, multiples, often aliased in the CMP domain, map in regions
of high q where the antialiasing operator is the most efficient.
In the next section, I investigate the effects of the
antialiasing operator when the radon domain is derived with a least-squares
approach.
noal
Figure 4 Left: The parabolic radon domain
after use of the antialising condition. The aliasing artifacts have decreased.
Right: The reconstructed data after the forward operator is applied
to the left panel.










Next: Operator antialiasing and least-squares
Up: antialiasing the parabolic radon
Previous: Computing the PRT in
Stanford Exploration Project
4/29/2001