




Next: Inversion of the Hessian
Up: Appendix
Previous: Appendix
Let us define the 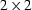 block matrix M as follows:
block matrix M as follows:
| 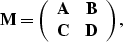 |
(18) |
where A, B, C, and D are matrices.
First, we consider the matrix equation
|  |
(19) |
If we multiply the top row by 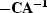 and add it to the bottom,
we have
and add it to the bottom,
we have
| 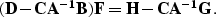 |
(20) |
Then we can easily find F and E. The quantity 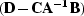 is called the Schur complement of A and,
denoted as
is called the Schur complement of A and,
denoted as 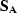 , appears often in linear algebra Demmel (1997).
The derivation of F and E can be written in a matrix form
, appears often in linear algebra Demmel (1997).
The derivation of F and E can be written in a matrix form
| 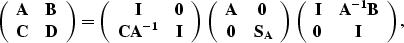 |
(21) |
which resembles an LDU decomposition of M.
Alternatively, we have the UDL decomposition
| 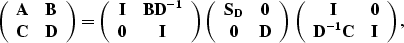 |
(22) |
where 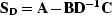 is the Schur complement of
D.
The inversion formulas are then easy to derive as follows:
is the Schur complement of
D.
The inversion formulas are then easy to derive as follows:
| 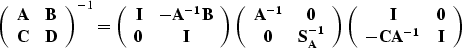 |
(23) |
and
| 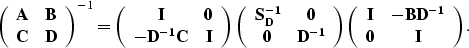 |
(24) |
The decomposition of the matrix M offers opportunities for
fast inversion algorithms. The final expressions for M are
| 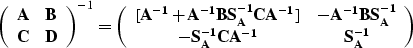 |
(25) |
and
| ![\begin{displaymath}
\left( \begin{array}
{cc}
{\bf A} & {\bf B} \\ {\bf C} & ...
...[{\bf D^{-1}}+{\bf
D^{-1}CS_D^{-1}BD^{-1}}]\end{array}\right).\end{displaymath}](img57.gif) |
(26) |
Equations (25) and (26) yield the matrix inversion lemma
| 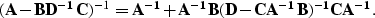 |
(27) |





Next: Inversion of the Hessian
Up: Appendix
Previous: Appendix
Stanford Exploration Project
4/29/2001