




Next: Tests
Up: Regularizing reflection seismic data
Previous: Regularizing reflection seismic data
A particularly efficient implementation of offset continuation results
from a log-stretch transform of the time coordinate
Bolondi et al. (1982), followed by a Fourier transform of the
stretched time axis. After these transforms,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) from Chapter
) from Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) takes
the form
takes
the form
| 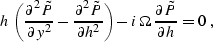 |
(125) |
where 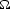 is the corresponding frequency, h is the half-offset,
y is the midpoint, and
is the corresponding frequency, h is the half-offset,
y is the midpoint, and 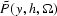 is the transformed
data Fomel (1995b, 2000b). As in other
F-X methods, equation (
is the transformed
data Fomel (1995b, 2000b). As in other
F-X methods, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be applied independently
and in parallel on different frequency slices.
) can be applied independently
and in parallel on different frequency slices.
Analogously to the case of the plane-wave-destructor filters discussed
in the previous section, we can construct an effective
offset-continuation finite-difference filter by studying first the
problem of wave extrapolation between neighboring offsets. In the
frequency-wavenumber domain, the extrapolation operator is defined in
accordance with equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), as follows:
), as follows:
| 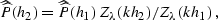 |
(126) |
where 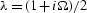 , and
, and 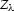 is the special
function defined in equation (
is the special
function defined in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The wavenumber k
corresponds to the midpoint y in the original data domain. In the
high-frequency asymptotics, operator (
). The wavenumber k
corresponds to the midpoint y in the original data domain. In the
high-frequency asymptotics, operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) takes the form
) takes the form
| ![\begin{displaymath}
\widehat{\widehat{P}}(h_2) = \widehat{\widehat{P}}(h_1)\,
F(...
...ga\,\psi\left(2 k h_2/\Omega - 2 k h_1/\Omega\right)\right]}\;,\end{displaymath}](img252.gif) |
(127) |
where functions F and 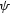 are defined in equations (
are defined in equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and (
)
and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
Returning to the original domain, I approximate the continuation
operator with a finite-difference filter of the form
| 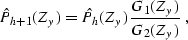 |
(128) |
which is somewhat analogous to (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The coefficients
of the filters G1(Zy) and G2(Zy) are found by fitting the
Taylor series coefficients of the filter response around the zero
wavenumber. In the simplest case of 3-point filters
). The coefficients
of the filters G1(Zy) and G2(Zy) are found by fitting the
Taylor series coefficients of the filter response around the zero
wavenumber. In the simplest case of 3-point filters![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) , this procedure uses four Taylor
series coefficients and leads to the following expressions:
, this procedure uses four Taylor
series coefficients and leads to the following expressions:
| 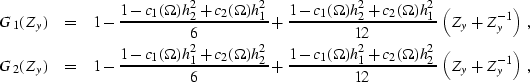 |
(129) |
| (130) |
where
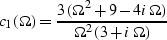
and
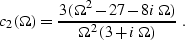
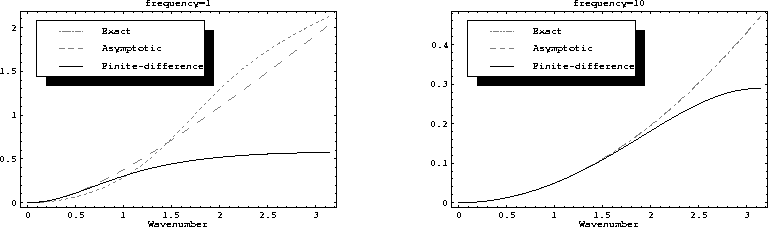
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the phase characteristic of the
finite-difference extrapolators (
compares the phase characteristic of the
finite-difference extrapolators (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the phase
characteristics of the exact operator (
) with the phase
characteristics of the exact operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the
asymptotic operator (
) and the
asymptotic operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The match between different
phases is poor for very low frequencies (left plot in
Figure
). The match between different
phases is poor for very low frequencies (left plot in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) but sufficiently accurate for frequencies in the
typical bandwidth of seismic data (right plot in
Figure
) but sufficiently accurate for frequencies in the
typical bandwidth of seismic data (right plot in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
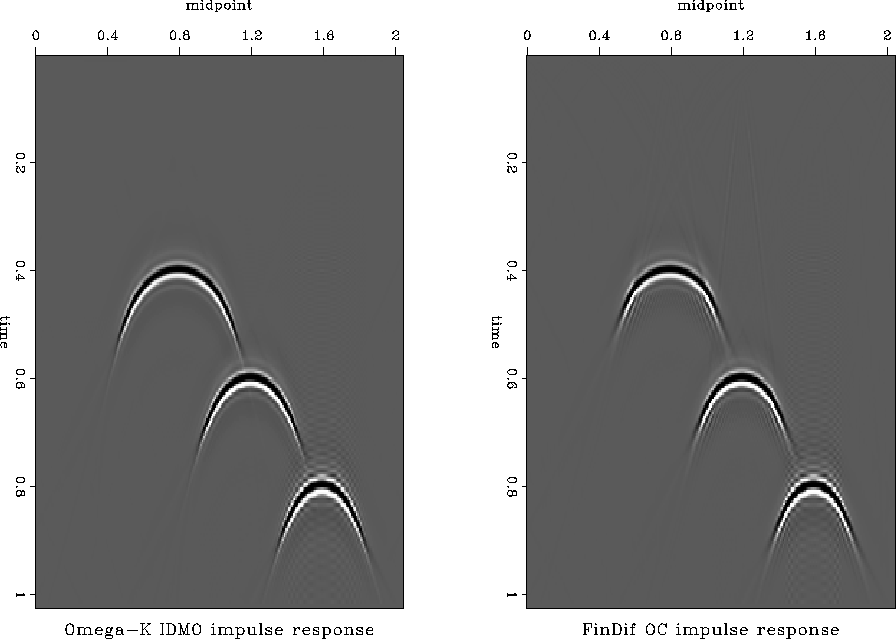
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares impulse responses of the inverse DMO
operator constructed by the asymptotic
compares impulse responses of the inverse DMO
operator constructed by the asymptotic  operator with those
constructed by finite-difference offset continuation. Neglecting
subtle phase inaccuracies at large dips, the two images look similar,
which indicates the high accuracy of the proposed finite-difference
scheme.
operator with those
constructed by finite-difference offset continuation. Neglecting
subtle phase inaccuracies at large dips, the two images look similar,
which indicates the high accuracy of the proposed finite-difference
scheme.
When applied on the offset-midpoint plane of an individual frequency
slice, the one-dimensional implicit filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
transforms to a two-dimensional explicit filter with the
2-D Z-transform
)
transforms to a two-dimensional explicit filter with the
2-D Z-transform
| 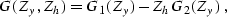 |
(131) |
analogous to filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for the case of local
plane-wave destruction. Convolution with filter (
) for the case of local
plane-wave destruction. Convolution with filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
the regularization operator that I propose for regularizing prestack
seismic data.
arg
) is
the regularization operator that I propose for regularizing prestack
seismic data.
arg
Figure 30 Phase of the implicit
offset-continuation operators in comparison with the exact solution.
The offset increment is assumed to be equal to the midpoint spacing.
The left plot corresponds to  , the right plot to
, the right plot to
 .
.




 off-imp
off-imp
Figure 31 Inverse DMO impulse responses
computed by the Fourier method (left) and by finite-difference
offset continuation (right). The offset is 1 km.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)










Next: Tests
Up: Regularizing reflection seismic data
Previous: Regularizing reflection seismic data
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) from Chapter
) from Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) takes
the form
takes
the form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) from Chapter
) from Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) takes
the form
takes
the form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be applied independently
and in parallel on different frequency slices.
) can be applied independently
and in parallel on different frequency slices.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), as follows:
), as follows:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The wavenumber k
corresponds to the midpoint y in the original data domain. In the
high-frequency asymptotics, operator (
). The wavenumber k
corresponds to the midpoint y in the original data domain. In the
high-frequency asymptotics, operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) takes the form
) takes the form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and (
)
and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The coefficients
of the filters G1(Zy) and G2(Zy) are found by fitting the
Taylor series coefficients of the filter response around the zero
wavenumber. In the simplest case of 3-point filters
). The coefficients
of the filters G1(Zy) and G2(Zy) are found by fitting the
Taylor series coefficients of the filter response around the zero
wavenumber. In the simplest case of 3-point filters![[*]](http://sepwww.stanford.edu/latex2html/foot_motif.gif) , this procedure uses four Taylor
series coefficients and leads to the following expressions:
, this procedure uses four Taylor
series coefficients and leads to the following expressions:
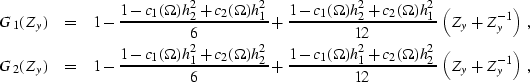
![]()
![]()
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares the phase characteristic of the
finite-difference extrapolators (
compares the phase characteristic of the
finite-difference extrapolators (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the phase
characteristics of the exact operator (
) with the phase
characteristics of the exact operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the
asymptotic operator (
) and the
asymptotic operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The match between different
phases is poor for very low frequencies (left plot in
Figure
). The match between different
phases is poor for very low frequencies (left plot in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) but sufficiently accurate for frequencies in the
typical bandwidth of seismic data (right plot in
Figure
) but sufficiently accurate for frequencies in the
typical bandwidth of seismic data (right plot in
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) compares impulse responses of the inverse DMO
operator constructed by the asymptotic
compares impulse responses of the inverse DMO
operator constructed by the asymptotic ![]() operator with those
constructed by finite-difference offset continuation. Neglecting
subtle phase inaccuracies at large dips, the two images look similar,
which indicates the high accuracy of the proposed finite-difference
scheme.
operator with those
constructed by finite-difference offset continuation. Neglecting
subtle phase inaccuracies at large dips, the two images look similar,
which indicates the high accuracy of the proposed finite-difference
scheme.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
transforms to a two-dimensional explicit filter with the
2-D Z-transform
)
transforms to a two-dimensional explicit filter with the
2-D Z-transform
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for the case of local
plane-wave destruction. Convolution with filter (
) for the case of local
plane-wave destruction. Convolution with filter (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
the regularization operator that I propose for regularizing prestack
seismic data.
) is
the regularization operator that I propose for regularizing prestack
seismic data.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)