




Next: Discussion
Up: Offset continuation for reflection
Previous: Offset continuation and DMO
The log-stretch transform, proposed by Bolondi et
al. 1982 and further developed by many
other researchers, has proven a useful tool in DMO
and OC processing. Applying a log-stretch transform of the form
| 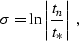 |
(254) |
where t* is an arbitrarily chosen time constant, eliminates the
time dependence of the coefficients in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and therefore makes this equation invariant to time shifts. After the
double Fourier transform with respect to the midpoint coordinate y
and to the transformed (log-stretched) time coordinate
)
and therefore makes this equation invariant to time shifts. After the
double Fourier transform with respect to the midpoint coordinate y
and to the transformed (log-stretched) time coordinate  , the
partial differential equation (
, the
partial differential equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) takes the form of
an ordinary differential equation,
) takes the form of
an ordinary differential equation,
| 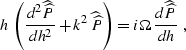 |
(255) |
where
| 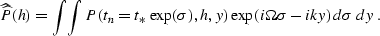 |
(256) |
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) has the known general solution,
expressed in terms of cylinder functions of complex order
) has the known general solution,
expressed in terms of cylinder functions of complex order 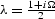 Watson (1952)
Watson (1952)
| 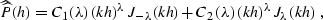 |
(257) |
where 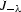 and
and 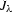 are Bessel functions, and C1
and C2 stand for some arbitrary functions of
are Bessel functions, and C1
and C2 stand for some arbitrary functions of  that do not
depend on k and h.
that do not
depend on k and h.
In the general case of offset continuation, C1 and C2 are
constrained by the two initial conditions (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In the special case of continuation from zero offset, we
can neglect the second term in (
). In the special case of continuation from zero offset, we
can neglect the second term in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as vanishing at the zero
offset. The remaining term defines the following operator of inverse
DMO in the
) as vanishing at the zero
offset. The remaining term defines the following operator of inverse
DMO in the 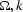 domain:
domain:
| 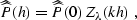 |
(258) |
where 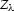 is the analytic function
is the analytic function
| 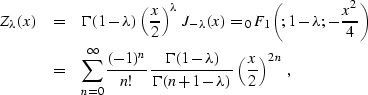 |
|
| (259) |
 is the gamma function and 0F1 is the confluent
hypergeometric limit function Petkovsek et al. (1996).
is the gamma function and 0F1 is the confluent
hypergeometric limit function Petkovsek et al. (1996).
The DMO operator now can be derived as the inversion of operator
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which is a simple multiplication by
), which is a simple multiplication by
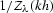 . Therefore, offset continuation becomes a
multiplication by
. Therefore, offset continuation becomes a
multiplication by 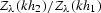 (the cascade
of two operators). This fact demonstrates an important advantage of
moving to the log-stretch domain: both offset continuation and DMO are simple
filter multiplications in the Fourier domain of the log-stretched time
coordinate.
(the cascade
of two operators). This fact demonstrates an important advantage of
moving to the log-stretch domain: both offset continuation and DMO are simple
filter multiplications in the Fourier domain of the log-stretched time
coordinate.
In order to compare operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the known versions
of log-stretch DMO, we need to derive its asymptotical representation
for high frequency
) with the known versions
of log-stretch DMO, we need to derive its asymptotical representation
for high frequency 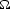 . The required asymptotic expression
follows directly from the definition of function
. The required asymptotic expression
follows directly from the definition of function 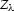 in
(
in
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the known asymptotical representation for a Bessel
function of high order Watson (1952):
) and the known asymptotical representation for a Bessel
function of high order Watson (1952):
| 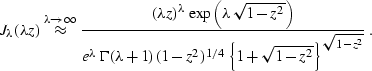 |
(260) |
Substituting approximation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into (
) into (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
considering the high-frequency limit of the resultant expression
yields
) and
considering the high-frequency limit of the resultant expression
yields
| 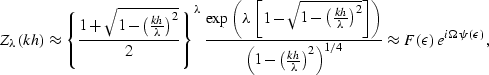 |
(261) |
where  denotes the ratio
denotes the ratio 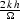 ,
,
| 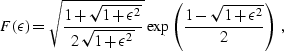 |
(262) |
and
| 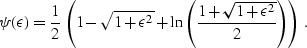 |
(263) |
Asymptotical representation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is valid for high
frequency
) is valid for high
frequency 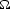 and
and 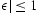 . It can be shown that the
phase function
. It can be shown that the
phase function 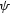 defined in (
defined in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) coincides precisely
with the analogous term in Liner's exact log DMO
Liner (1990), which was proven to provide the correct
geometric properties of DMO. Similar expressions for the log-stretch
phase factor
) coincides precisely
with the analogous term in Liner's exact log DMO
Liner (1990), which was proven to provide the correct
geometric properties of DMO. Similar expressions for the log-stretch
phase factor 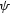 were derived in different ways by
Zhou et al. (1996) and Canning and Gardner (1996).
However, the amplitude term
were derived in different ways by
Zhou et al. (1996) and Canning and Gardner (1996).
However, the amplitude term 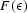 differs from the previously
published ones because of the difference in the amplitude preservation
properties.
differs from the previously
published ones because of the difference in the amplitude preservation
properties.
A number of approximate log DMO operators have been proposed in the
literature. As shown by Liner (1990), all of them but
exact log DMO distort the geometry of reflection effects at large
offsets. The distortion is caused by the implied approximations of the
true phase function 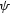 . Bolondi's OC operator
Bolondi et al. (1982) implies
. Bolondi's OC operator
Bolondi et al. (1982) implies 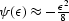 , Notfors' DMO Notfors and Godfrey (1987) implies
, Notfors' DMO Notfors and Godfrey (1987) implies
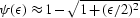 , and the ``full
DMO'' Bale and Jakubowicz (1987) has
, and the ``full
DMO'' Bale and Jakubowicz (1987) has ![$\psi(\epsilon) \approx {1 \over 2}
\ln\left[1-(\epsilon / 2)^2\right]$](img458.gif) . All these approximations are
valid for small
. All these approximations are
valid for small  (small offsets or small reflector dips) and
have errors of the order of
(small offsets or small reflector dips) and
have errors of the order of 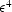 (Figure
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The
range of validity of Bolondi's operator is defined in
equation (
). The
range of validity of Bolondi's operator is defined in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
pha
Figure 8 Phase functions of the log
DMO operators. Solid line: exact log DMO; dashed line: Bolondi's
OC; dashed-dotted line: Bale's full DMO; dotted line: Notfors'
DMO.
|
|  |





In practice, seismic data are often irregularly sampled in space but
regularly sampled in time. This makes it attractive to apply offset
continuation and DMO operators in the 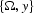 domain, where
the frequency
domain, where
the frequency 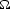 corresponds to the log-stretched time and
y is the midpoint coordinate. Performing the inverse Fourier
transform on the spatial frequency transforms the inverse DMO
operator (
corresponds to the log-stretched time and
y is the midpoint coordinate. Performing the inverse Fourier
transform on the spatial frequency transforms the inverse DMO
operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the
) to the  domain, where the
filter multiplication becomes a convolutional operator:
domain, where the
filter multiplication becomes a convolutional operator:
|  |
(264) |
Here  is a high-pass frequency filter:
is a high-pass frequency filter:
|  |
(265) |
At high frequencies 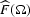 is approximately equal to
is approximately equal to
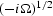 , which corresponds to the half-derivative
operator
, which corresponds to the half-derivative
operator 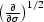 , which,
in turn, is equal to the
, which,
in turn, is equal to the 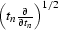 term of the asymptotical OC
operator (
term of the asymptotical OC
operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The difference between the exact
filter
). The difference between the exact
filter 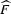 and its approximation by the half-order
derivative operator is shown in Figure
and its approximation by the half-order
derivative operator is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . This difference
is a measure of the validity of asymptotical OC operators.
flt
. This difference
is a measure of the validity of asymptotical OC operators.
flt
Figure 9 Amplitude (left) and phase (right) of
the time filter in the log-stretch domain. The solid line is for the
exact filter; the dashed line for its approximation by the
half-order derivative filter.





Inverting operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can obtain the DMO operator in the
), we can obtain the DMO operator in the
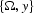 domain.
domain.





Next: Discussion
Up: Offset continuation for reflection
Previous: Offset continuation and DMO
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
and therefore makes this equation invariant to time shifts. After the
double Fourier transform with respect to the midpoint coordinate y
and to the transformed (log-stretched) time coordinate
)
and therefore makes this equation invariant to time shifts. After the
double Fourier transform with respect to the midpoint coordinate y
and to the transformed (log-stretched) time coordinate ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) takes the form of
an ordinary differential equation,
) takes the form of
an ordinary differential equation,
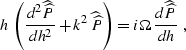
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) has the known general solution,
expressed in terms of cylinder functions of complex order
) has the known general solution,
expressed in terms of cylinder functions of complex order ![]() Watson (1952)
Watson (1952)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In the special case of continuation from zero offset, we
can neglect the second term in (
). In the special case of continuation from zero offset, we
can neglect the second term in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as vanishing at the zero
offset. The remaining term defines the following operator of inverse
DMO in the
) as vanishing at the zero
offset. The remaining term defines the following operator of inverse
DMO in the ![]() domain:
domain:
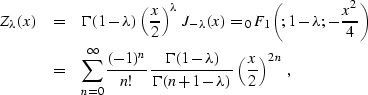
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which is a simple multiplication by
), which is a simple multiplication by
![]() . Therefore, offset continuation becomes a
multiplication by
. Therefore, offset continuation becomes a
multiplication by ![]() (the cascade
of two operators). This fact demonstrates an important advantage of
moving to the log-stretch domain: both offset continuation and DMO are simple
filter multiplications in the Fourier domain of the log-stretched time
coordinate.
(the cascade
of two operators). This fact demonstrates an important advantage of
moving to the log-stretch domain: both offset continuation and DMO are simple
filter multiplications in the Fourier domain of the log-stretched time
coordinate.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the known versions
of log-stretch DMO, we need to derive its asymptotical representation
for high frequency
) with the known versions
of log-stretch DMO, we need to derive its asymptotical representation
for high frequency ![]() . The required asymptotic expression
follows directly from the definition of function
. The required asymptotic expression
follows directly from the definition of function ![]() in
(
in
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the known asymptotical representation for a Bessel
function of high order Watson (1952):
) and the known asymptotical representation for a Bessel
function of high order Watson (1952):
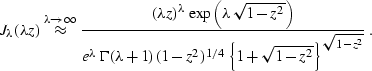
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into (
) into (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
considering the high-frequency limit of the resultant expression
yields
) and
considering the high-frequency limit of the resultant expression
yields
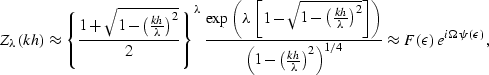
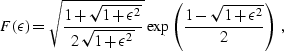
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is valid for high
frequency
) is valid for high
frequency ![]() and
and ![]() . It can be shown that the
phase function
. It can be shown that the
phase function ![]() defined in (
defined in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) coincides precisely
with the analogous term in Liner's exact log DMO
Liner (1990), which was proven to provide the correct
geometric properties of DMO. Similar expressions for the log-stretch
phase factor
) coincides precisely
with the analogous term in Liner's exact log DMO
Liner (1990), which was proven to provide the correct
geometric properties of DMO. Similar expressions for the log-stretch
phase factor ![]() were derived in different ways by
Zhou et al. (1996) and Canning and Gardner (1996).
However, the amplitude term
were derived in different ways by
Zhou et al. (1996) and Canning and Gardner (1996).
However, the amplitude term ![]() differs from the previously
published ones because of the difference in the amplitude preservation
properties.
differs from the previously
published ones because of the difference in the amplitude preservation
properties.
![]() . Bolondi's OC operator
Bolondi et al. (1982) implies
. Bolondi's OC operator
Bolondi et al. (1982) implies ![]() , Notfors' DMO Notfors and Godfrey (1987) implies
, Notfors' DMO Notfors and Godfrey (1987) implies
![]() , and the ``full
DMO'' Bale and Jakubowicz (1987) has
, and the ``full
DMO'' Bale and Jakubowicz (1987) has ![]() . All these approximations are
valid for small
. All these approximations are
valid for small ![]() (small offsets or small reflector dips) and
have errors of the order of
(small offsets or small reflector dips) and
have errors of the order of ![]() (Figure
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The
range of validity of Bolondi's operator is defined in
equation (
). The
range of validity of Bolondi's operator is defined in
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).

![]() domain, where
the frequency
domain, where
the frequency ![]() corresponds to the log-stretched time and
y is the midpoint coordinate. Performing the inverse Fourier
transform on the spatial frequency transforms the inverse DMO
operator (
corresponds to the log-stretched time and
y is the midpoint coordinate. Performing the inverse Fourier
transform on the spatial frequency transforms the inverse DMO
operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the
) to the ![]() domain, where the
filter multiplication becomes a convolutional operator:
domain, where the
filter multiplication becomes a convolutional operator:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The difference between the exact
filter
). The difference between the exact
filter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) . This difference
is a measure of the validity of asymptotical OC operators.
. This difference
is a measure of the validity of asymptotical OC operators.
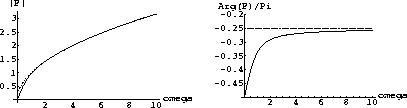
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can obtain the DMO operator in the
), we can obtain the DMO operator in the
![]() domain.
domain.